大家好，我是肆〇柒。今天要和大家分享一篇由Google DeepMind与约翰霍普金斯大学联合研究的重要论文《On the Theoretical Limitations of Embedding-Based Retrieval》。这项研究揭示了一个令人震惊的事实：即使是"谁喜欢考拉袋鼠？"这样简单的查询，也可能超出当前最先进嵌入模型的能力范围——不是因为模型不够"智能"，也不是训练数据不足，而是源于向量空间本身的数学特性所决定的根本限制。当我们在搜索框中输入越来越复杂的指令时，可能正在不知不觉中触碰这些理论边界。接下来，让我们深入探索这一发现如何重塑我们对信息检索技术的理解，以及它对下一代搜索系统设计的深远影响。
LIMIT数据集创建过程
"你是否曾经在搜索引擎中输入'适合家庭的海滩度假地，靠近动物园但远离嘈杂夜店'，却发现结果总是不理想？ 这可能不是因为算法"不够聪明"，而是源于搜索技术无法逾越的数学本质限制。最新研究《On the Theoretical Limitations of Embedding-Based Retrieval》揭示：即使是"谁喜欢考拉袋鼠？"这样简单的查询，也可能超出当前最先进搜索模型的能力范围——不是因为模型不够"智能"，而是向量空间本身的数学特性决定了这种根本限制。
理论基础与数学本质
从日常搜索到几何限制
想象一下，你正在计划一次家庭度假，需要搜索"适合家庭的海滩度假地，靠近动物园但远离嘈杂夜店"。这个查询包含了多个条件，需要模型将原本不相关的文档（海滩度假地、动物园、夜店）连接起来。然而，最新研究表明，当查询需要连接的文档组合数量超过某个阈值时，即使是最先进的Embedding模型也会束手无策。
向量嵌入已成为现代信息检索的核心技术，从传统的关键词匹配发展到如今支持指令跟随、逻辑推理等复杂任务。然而，这些Embedding模型本质上是在几何空间中操作，而几何空间有着固有的表达能力限制。当模型试图用向量表示查询和文档，并通过点积计算相关性时，它们实际上是在尝试用有限维度的空间捕获无限可能的相关性关系。
关键洞察在于，嵌入维度d直接决定了模型能表示的top-k文档组合数量。研究证明，对于给定的嵌入维度d，存在某些top-k文档组合无法被任何查询返回——无论查询如何设计。这并非模型训练不足的问题，而是向量空间本身的数学特性所决定的。正如论文所言："there exists top-k combinations of documents that cannot be returned—no matter the query"。（无论怎么查询，总会有一些排名前k的文档组合是返回不了的）
为什么这些限制不可避免
为了直观理解这一概念，可以想象一个d维空间中的"蛋糕切割"问题：每个查询定义了一种切割方式，将文档空间分割成相关与不相关区域。rankrop A表示能够实现所有可能切割所需的最少维度。当文档组合数量超过维度能力时，就像试图用有限刀数切割无限种蛋糕形状，某些特定组合将无法实现。这一限制与蛋糕本身（查询内容）无关，而是由切割工具（嵌入维度）的物理特性决定。
关键收获：论文明确指出："for web-scale search, even the largest embedding dimensions with ideal test-set optimization are not enough to model all combinations"(对于网络规模的搜索任务，即便采用最大的嵌入维度，并通过理想化的测试集进行优化，仍不足以建模所有可能的组合)。
这意味着即使在理想条件下（直接优化测试集向量），现有最大维度的Embedding模型也无法处理大规模检索场景中的所有可能组合。这不是训练数据或模型规模的问题，而是向量空间本身的数学特性所决定的根本限制。
临界点：维度与能力的精确关系
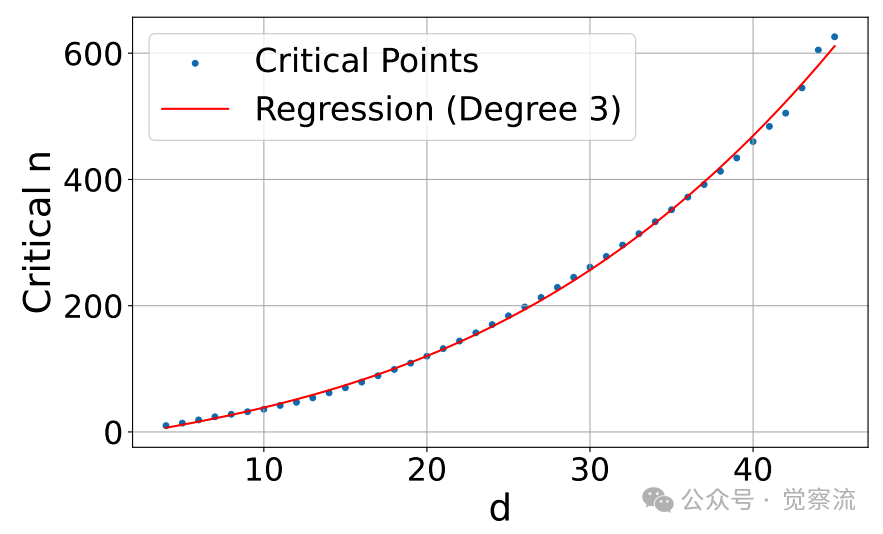
临界文档数量与嵌入维度的三次多项式关系
上图直观展示了嵌入维度与模型能处理的最大文档数量之间的非线性关系。图表显示，临界文档数量n与维度d的关系可精确拟合为三次多项式：n ≈ -10.53 + 4.03d + 0.052d² + 0.0037d³ (r²=0.999)。例如：
- 512维模型最多只能处理约50万文档
- 768维模型约170万文档
- 1024维模型约400万文档
- 4096维模型也仅能处理约2.5亿文档
这就像试图用有限的折叠次数表示无限可能的路线——当文档数量增加，组合爆炸会让任何固定维度的模型力不从心。正如研究通过自由嵌入优化实验所证实的，这些限制不可避免，因为增加维度只能线性扩展表示能力，而组合复杂度呈指数增长。
理论验证：从数学到实证
自由嵌入优化：最佳情况测试
为了证明这些限制是根本性的而非训练不足造成的，研究设计了"自由嵌入"优化实验。在这种设置中，查询和文档向量直接通过梯度下降优化，完全排除了自然语言约束和训练数据限制。这表明了任何Embedding模型是否能够解决该问题：如果自由嵌入优化无法解决该问题，那么实际的检索模型也无法解决。
实验聚焦于k=2的情况，逐步增加文档数量n直到优化无法达到100%准确率，记录这一"临界-n"点。Figure 2展示了临界-n值与嵌入维度的关系，完美拟合三次多项式曲线。
关键发现包括：
- 512维模型的临界-约为50万
- 4096维模型约为2.5亿
这表明即使在最佳情况下（直接优化测试集向量），现有最大维度的Embedding模型也无法处理大规模检索场景中的所有可能组合。这一结果验证了理论预测：当文档数量超过临界点时，即使在理想条件下也无法表示所有top-2组合。
LIMIT数据集：理论到实践的精确映射
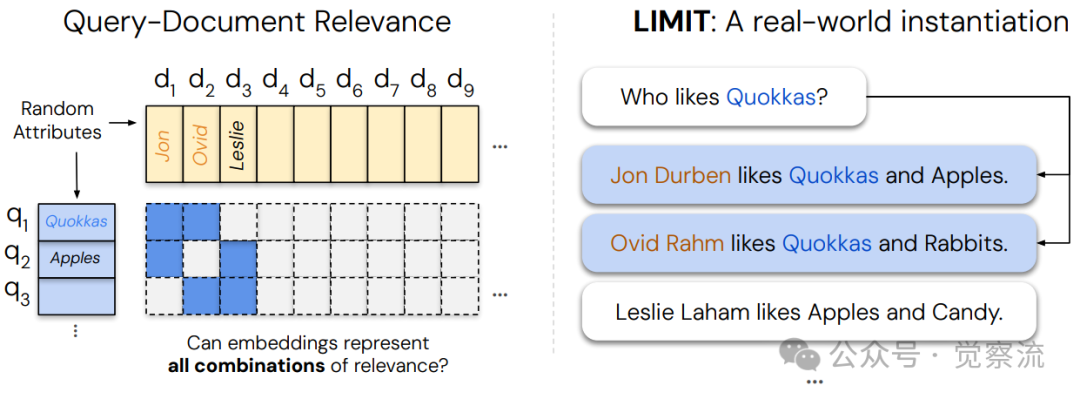
为了将理论限制映射到真实语言环境，研究创建了LIMIT数据集。其设计原理比较巧妙：
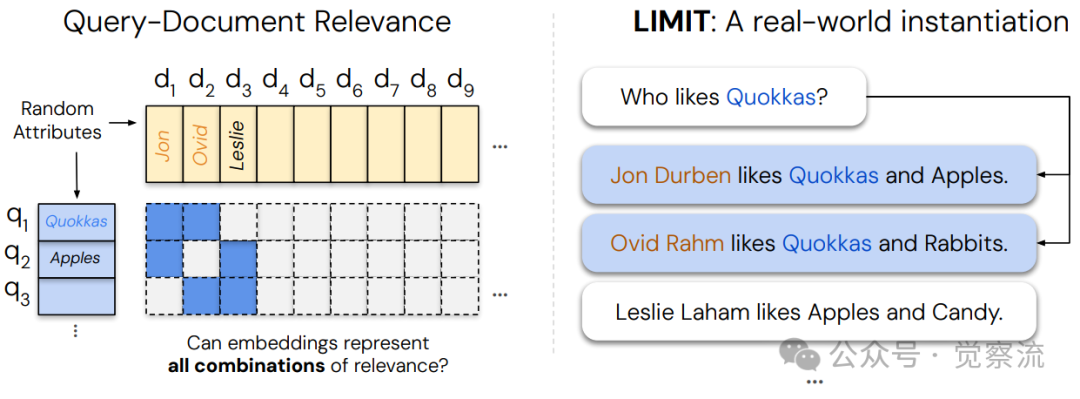LIMIT数据集创建过程
LIMIT数据集巧妙设计了46个文档，因为从46个文档中任选2个的组合数为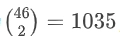
，这是能产生超过1000个查询的最小文档集。想象一下，如果每个文档代表一个人，每个查询"谁喜欢X？"对应两个喜欢特定物品的人，那么我们需要测试所有可能的两人组合（如"谁喜欢考拉袋鼠？"、"谁喜欢苹果？"等），总共1035种情况。这种设计将抽象的理论限制精确映射到极其简单的自然语言任务中。
研究还引入了"查询强度"（Average Query Strength）指标来量化数据集的组合密度。该指标将qrel矩阵视为查询-查询图，计算每个查询节点的强度（与之共享相关文档的其他查询的加权和），然后取平均值。
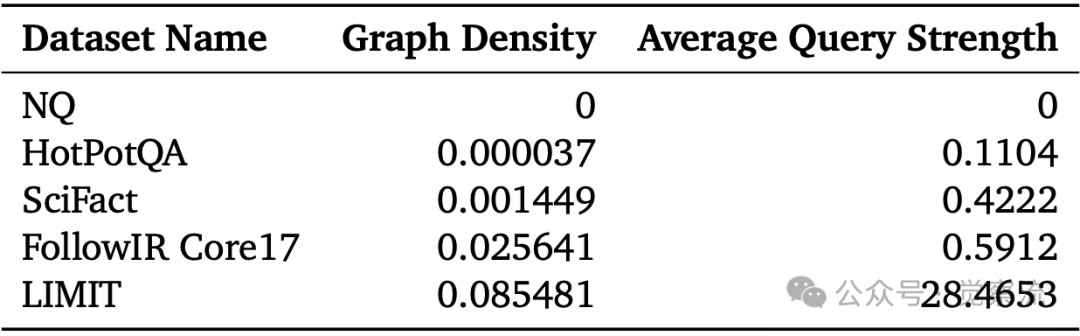
不同数据集的组合复杂度指标对比
LIMIT数据集的Graph Density（0.085）和Average Query Strength（28.47）远超常规数据集（如BEIR的0.59）。这就像社交网络：在LIMIT中，平均每个"查询节点"与其他28个查询共享相关文档，形成密集连接的"社交圈"；而在BEIR中，每个查询平均只与不到1个其他查询有联系，网络极为稀疏。这种密集连接正是导致Embedding模型失效的关键原因——模型无法在有限维度空间中表示如此复杂的文档关系网络。
实验结果
在LIMIT数据集上的实验结果触目惊心：
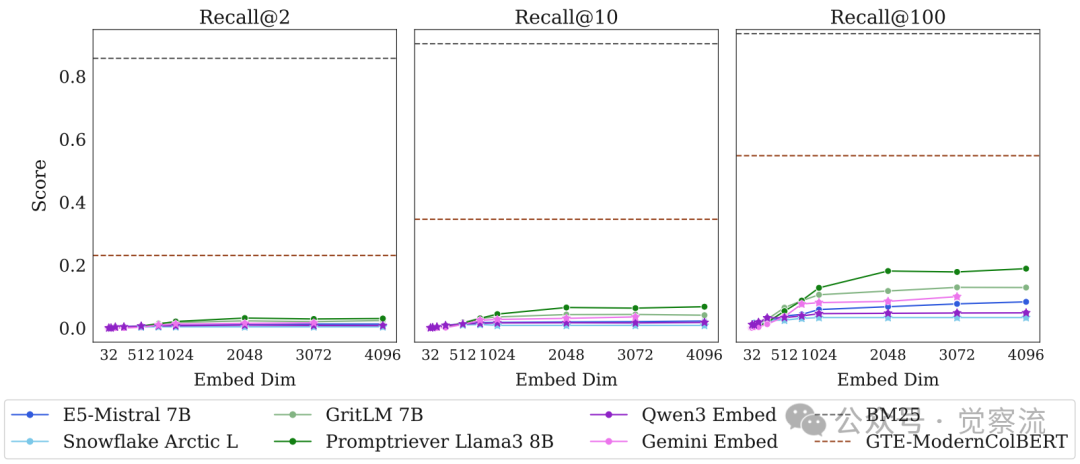
LIMIT完整任务上的模型表现
上图揭示了惊人的事实：在完整LIMIT任务（50k文档）中，即使是最高维度的Embedding模型表现也极为有限。Promptriever（4096维）的Recall@100仅为18.9%，GritLM为12.9%，而Gemini Embeddings仅为10.0%。这意味着当搜索"谁喜欢考拉袋鼠？"时，模型只能在前100个结果中找到不到20个真正喜欢考拉袋鼠的人。
相比之下，传统BM25方法达到了93.6%的Recall@100，几乎完美解决了这个看似简单的任务。这种巨大差距不是因为现代模型"不够智能"，而是因为任务本身的组合复杂度超出了向量空间的数学表达能力。就像试图用二维地图精确表示三维地形一样，某些信息注定会丢失。
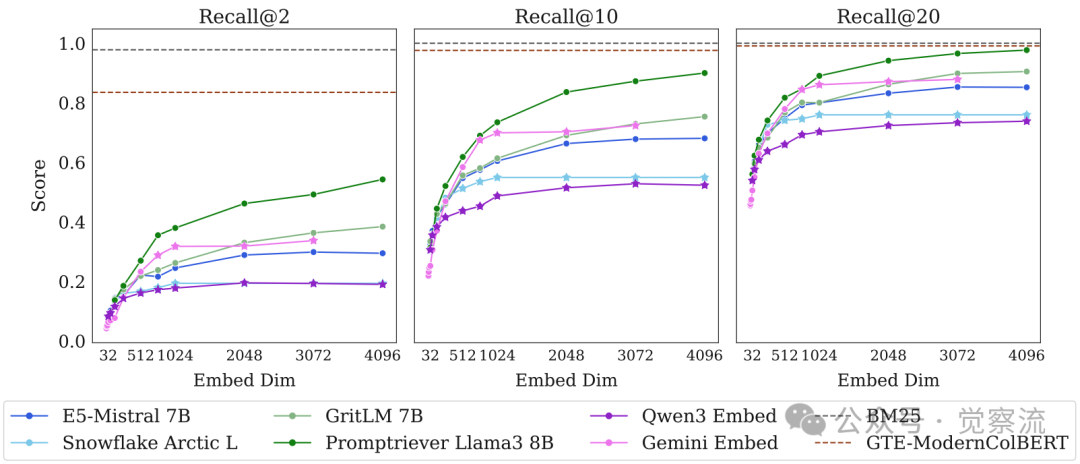
LIMIT小规模任务上的模型表现
在仅46文档的简化版LIMIT上（上图），模型甚至无法在Recall@20上达到完美表现。即使是4096维的Promptriever模型，其Recall@20也仅达到97.7%，远低于BM25的100%。
更关键的是，模型性能与嵌入维度呈强正相关，完美验证了理论预测。高维度模型（如4096维的Promptriever）表现显著优于低维度模型（如32维的Qwen3 Embed），但即使最高维度也无法完全解决任务。
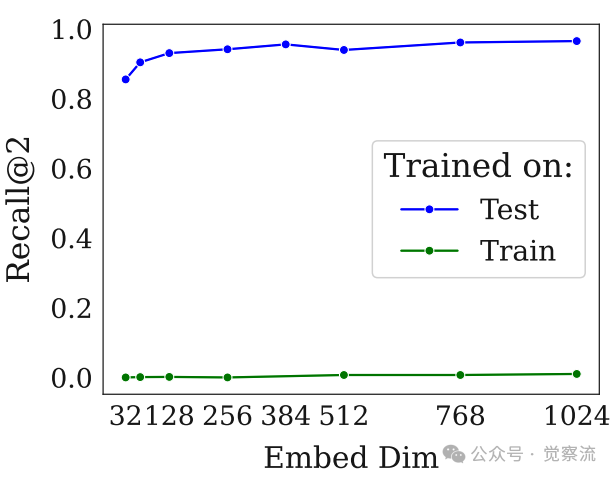
训练集vs测试集实验结果
上图的对比实验提供了关键证据：当模型在LIMIT训练集上训练时，Recall@10仅从0提升到2.8，而直接在测试集上训练则能近乎完美解决问题。这明确表明问题本质是理论限制而非领域适应性问题——在领域内训练时缺乏性能提升表明，性能不佳并非由于领域偏移所致。
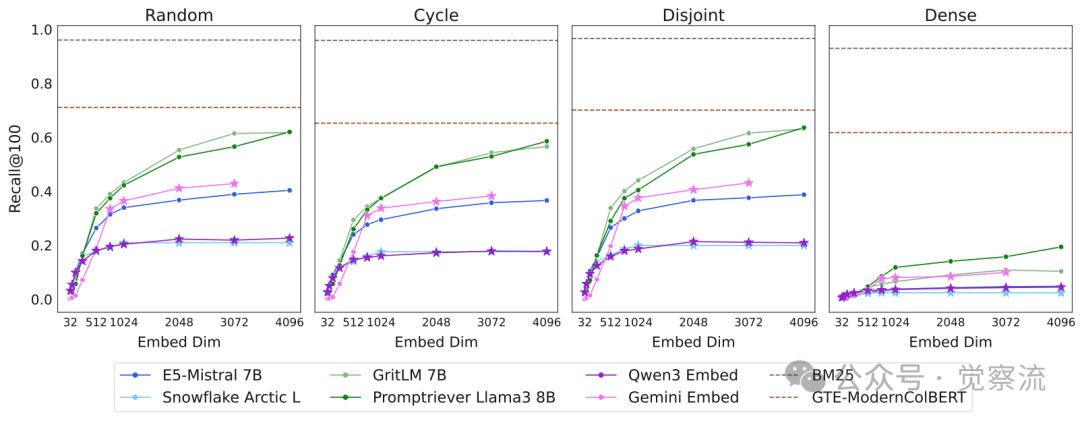
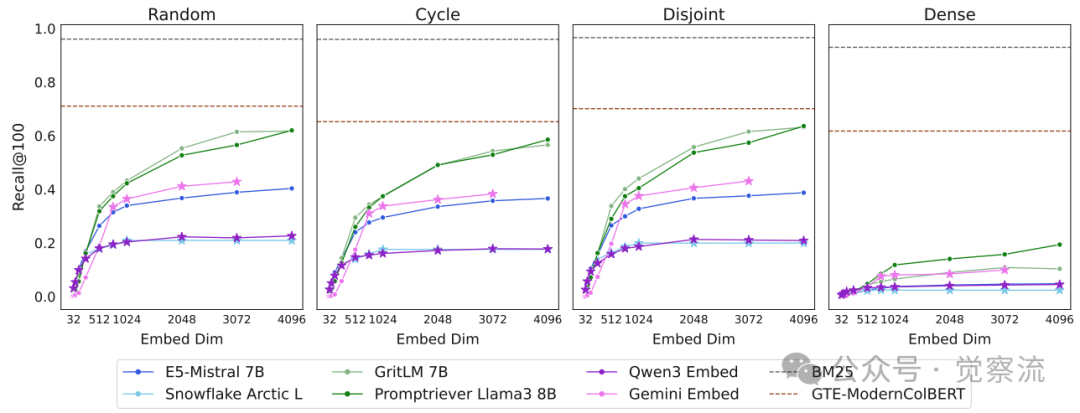
不同qrel模式下的模型表现对比
上图的实验结果揭示了组合密度对任务难度的决定性影响。研究创建了四种qrel模式：随机、循环、不相交和密集（所有可能组合）。数据显示：
- 密集模式比其他模式难10倍以上
- GritLM在密集模式下的Recall@100仅为10.4%
- 而在其他模式下均超过50%
这一发现验证了理论预测：文档组合的"互联程度"（graph density）是决定任务难度的关键因素。
对检索领域的深远影响
指令跟随能力的双刃剑效应
随着指令跟随检索的兴起，模型被要求处理"any query and any notion of relevance"，这极大地放大了组合复杂度问题。例如，当用户查询"适合家庭的海滩度假地，靠近动物园但远离嘈杂夜店"时，模型需要连接原本不相关的文档集合。
逻辑操作符的指数效应
逻辑操作符对组合复杂度的影响远超直觉：
- 单独搜索"海滩度假地"：可能有1000个相关结果
- 单独搜索"靠近动物园"：可能有500个相关结果
- 但搜索"海滩度假地 AND 靠近动物园"：相关结果可能不是1500个，而是呈指数级增长的组合空间
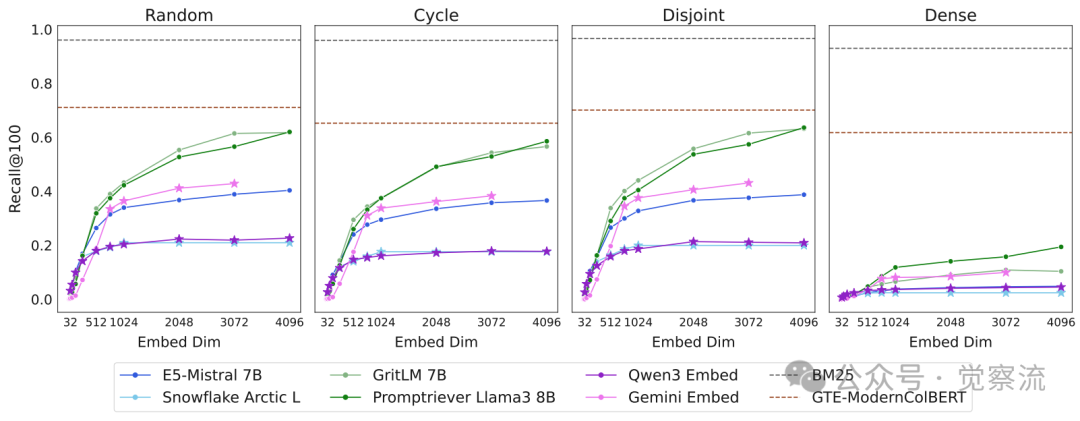
不同qrel模式下的模型表现对比
上图清晰展示了这一效应：在密集组合模式下，即使是最高级的Embedding模型（如GritLM），Recall@100也仅能达到10.4%，而在其他模式下可超过50%。
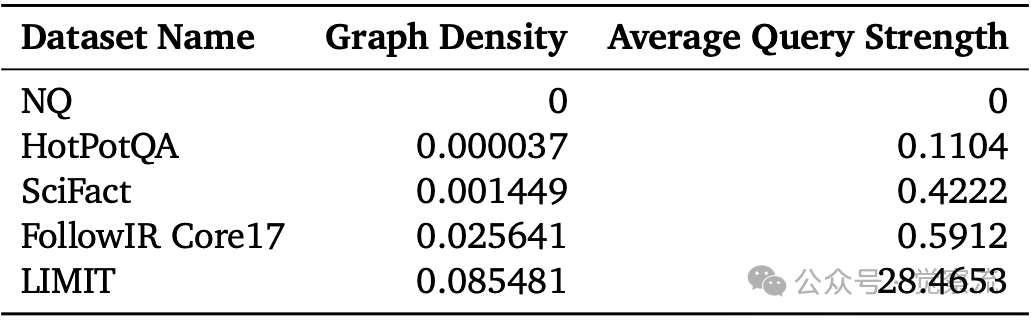
上表显示，FollowIR Core17（指令跟随数据集）的Graph Density(0.0256)和Average Query Strength(0.59)已显著高于传统数据集，但远低于LIMIT(0.0855和28.47)，表明更复杂的指令将快速逼近理论边界。
能力提升反而加剧问题
指令跟随能力的提升反而加剧了这一问题，因为更强大的指令理解能力使用户能更精确地指定复杂的相关性关系，从而需要模型表示更多样的文档组合。
特别是，现代搜索工具（如BrowseComp）允许用户通过多个条件组合精确选择任意top-k集合，这使得实际使用中更容易触及这些限制。研究指出，随着任务要求返回越来越多的前k个相关文档的组合（例如，通过指令将先前无关的文档用逻辑运算符连接起来），我们正快速接近Embedding模型的理论极限。
模型能力的重新评估框架
研究提供了评估模型能力的新视角。例如，Promptriever等指令微调模型表现更好，可能是因为他们的训练，使他们能够利用更多的嵌入维度，而不仅仅是任务覆盖更广。
值得注意的是，模型维度效率存在显著差异：
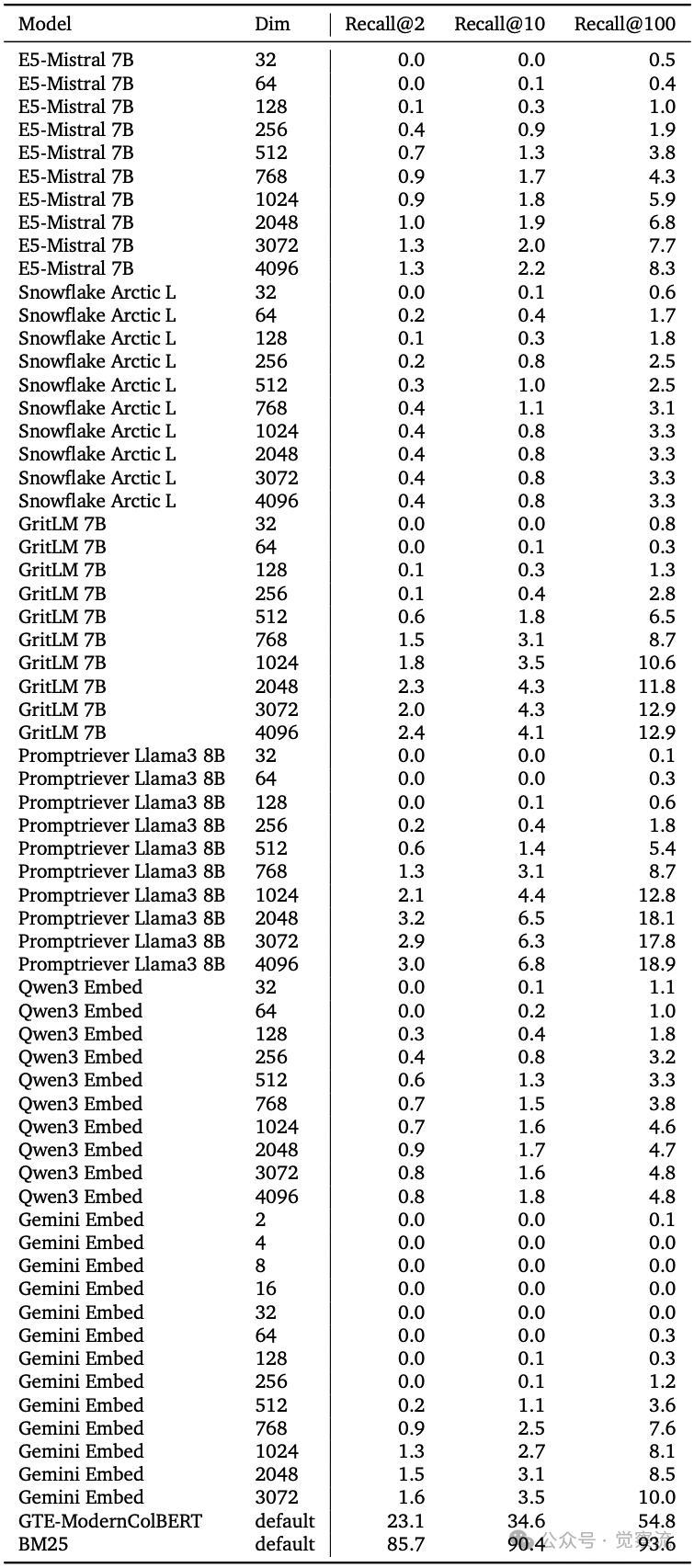
不同模型在LIMIT上的性能对比
上表显示，尽管Gemini Embeddings拥有4096维，但其在LIMIT上的表现不如维度更低但训练更优化的Promptriever。在4096维时，Promptriever的LIMIT Recall@100达到18.9，而Gemini Embed仅10.0。这表明，模型能否有效利用其全部维度可能是比绝对维度更重要的因素。
研究还挑战了"更多数据和更好训练能解决所有问题"的假设。即使有无限训练数据，模型仍无法表示超出其维度能力的文档组合。正如论文强调的："there exists top-k combinations of documents that cannot be returned—no matter the query"（存在一种情况，一些文档的前k个组合，无论查询如何，都无法被召回）。
超越限制：实用解决方案
架构选择的精确权衡
面对这些理论限制，研究评估了不同检索架构的优劣：
单向量Embedding模型：适合组合空间有限的场景，但需警惕其理论边界。当任务涉及大量文档组合时，即使SOTA模型也会严重受限。
稀疏模型（BM25）：作为传统方法，BM25在LIMIT上接近完美表现（Recall@100达93.6%）。这是因为其有效维度极高——词汇表大小（通常数万）作为"维度"，使其能表示更多文档组合。Table 3显示，BM25在各种qrel模式下均保持93%以上的Recall@100。BM25 表现非常出色，因为其具有更高的维度。然而，这种高维度优势在指令跟随任务中可能失效，如何将稀疏模型应用于指令遵循和基于推理的任务尚不明确，因为在这些任务中，既没有词汇上的重叠，甚至也没有类似释义的重叠。
多向量模型（GTE-ModernColBERT）：这类模型通过每个序列使用多个向量并结合MaxSim操作符，显著提高了表达能力。Table 4显示，在46文档小规模LIMIT上，GTE-ModernColBERT的Recall@2达到83.5%，远超单向量模型。这是因为多向量模型本质上增加了"有效维度"——每个token有自己的向量表示，然后通过MaxSim聚合，使模型能捕获更复杂的文档特征组合。然而，研究也指出，这些模型通常不用于指令遵循或基于推理的任务，其适用性仍需验证。
交叉编码器的精准定位
研究测试了长上下文重排序器Gemini-2.5-Pro在46文档LIMIT小规模版上的表现，结果令人惊讶：它能在一次前向传递中100%解决所有1000个查询，而最佳Embedding模型的Recall@2甚至不足60%。
这一结果突显了交叉编码器的关键优势：对于最先进的重排序模型来说，LIMIT 是简单的，因为它们不受嵌入维度的限制。这就能更灵活地建模查询-文档关系。
然而，交叉编码器的计算成本，使其不适合大规模的第一阶段检索。在实际系统中，更可行的策略是使用单向量模型进行初筛，再用交叉编码器对候选集进行精排。
面向未来的检索系统设计
基于这些发现，研究提出了几项实用建议：
不同qrel模式下的模型表现对比
为在实际系统中监测是否接近理论边界，建议实施以下监控机制：
1. 简单查询性能监控：定期测试类似"谁喜欢考拉袋鼠？"的简单查询，若Recall@100持续低于20%，则可能已触及理论边界
2. 维度扩展测试：当系统升级到更高维度模型时，若性能提升幅度远低于预期（如从768维升级到1024维仅提升2-3%），则表明接近维度瓶颈
3. 组合复杂度评估：计算系统中查询的Graph Density和Average Query Strength，当这些指标超过常规阈值（如Average Query Strength > 5）时，应考虑架构转换
一旦检测到这些信号，可自动切换至混合检索策略——对高复杂度查询使用交叉编码器精排，而对简单查询继续使用高效单向量模型。
具体实施指南：
- 当用户查询包含"AND"、"OR"等逻辑操作符时
- 当查询包含多个条件（如"价格低于$200 AND 评分高于4星 AND 免费送货"）时
- 当系统检测到查询需要连接原本不相关的文档集合时
未来应致力于开发能够解决这一根本局限性的方法。特别是能处理任何查询和相关性定义的新范式。论文特别强调：实践中，在设计评估时（如LIMIT所示）以及选择替代的检索方法时，都应意识到这些局限性。这不仅关乎模型选择，更影响整个检索系统的架构设计。
总结
现在思考一个问题：你最近一次搜索中，是否曾尝试输入一个包含多个条件的复杂查询？结果是否令你满意？根据本文内容，这可能不是因为搜索引擎"不够聪明"，而是因为你的查询已经触及了当前技术的理论边界。
下次当你输入类似"适合家庭的海滩度假地，靠近动物园但远离嘈杂夜店"的查询时，不妨尝试将其拆分为多个简单查询，可能会获得更好的结果——这不是你的错，而是当前技术的数学本质限制。
Embedding模型的理论限制不是"如果"而是"何时"会遇到的问题。随着任务要求召回越来越多的前k个相关文档的组合，我们终将触及这些边界。LIMIT数据集的创建正是为了揭示这一现实：即使是简单的查询，也可能超出当前最先进模型的能力范围。
这项研究的核心价值在于将抽象的数学限制与实际检索性能联系起来，提供了可量化的理论框架和实证验证。它提醒我们，模型进步不应仅关注规模扩大，而应从根本上解决这些"fundamental limitation"。
对于 AI 应用落地的开发者而言，这意味着需要重新思考评估标准、模型选择和系统设计。在构建下一代检索系统时，必须考虑任务的组合复杂度，并在单向量嵌入、多向量模型和交叉编码器之间做出明智权衡。
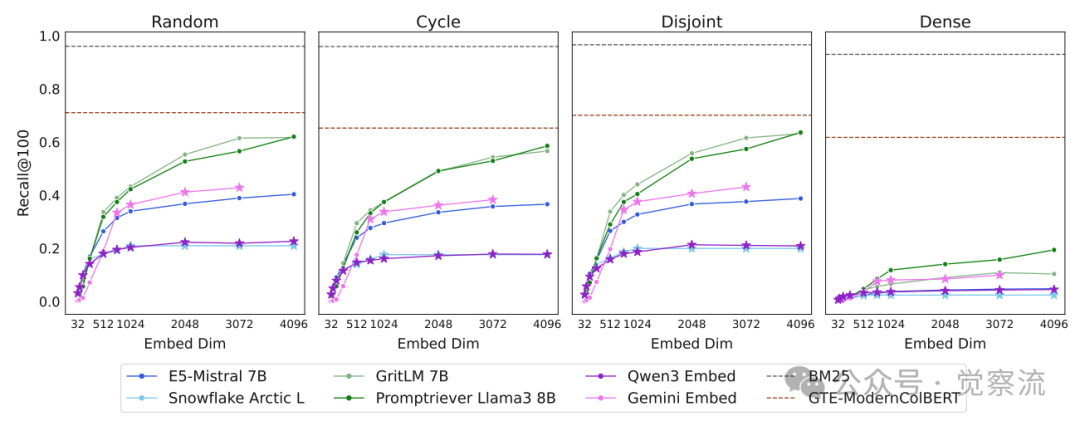
实践中，可通过三个信号判断是否接近理论边界：1）在简单查询上性能异常低下（如"谁喜欢考拉袋鼠？"类查询Recall@100<20%）；2）增加嵌入维度带来持续但有限的性能提升；3）在密集qrel模式下性能骤降（如下图所示）。当这些信号出现时，应考虑架构转换——对高组合复杂度查询自动切换至交叉编码器，或采用混合检索策略。
只有我们正视这些理论边界，才能设计出真正强大的信息检索系统，超越维度的限制，抵达更广阔的智能检索未来。
