系统梳理 Test-Time Compute 的主要实现路径

当前大语言模型（LLM）最有趣的研究趋势之一，是推理模型的兴起 —— 这类模型在给出答案前会花费时间进行思考。

这种技术通常被称为「测试时计算」（test-time compute），即在推理阶段进行深度推理。其实在模型推理过程中应用搜索或深度推理的思路早已存在（例如 AlphaZero[1]，以及 Transformer 诞生之前就尝试用类似方法解决旅行商问题的论文[2]），但 o1 的出现让这一理念重新回到了主流视野。

最令人兴奋的是，这种测试时计算可能展现出与预训练相似的扩展规律 —— 换言之，就像增加训练计算量能带来模型能力的指数级提升一样，若在推理阶段分配更多计算资源（延长思考时间），模型性能理论上也会出现可预测的指数级增长。

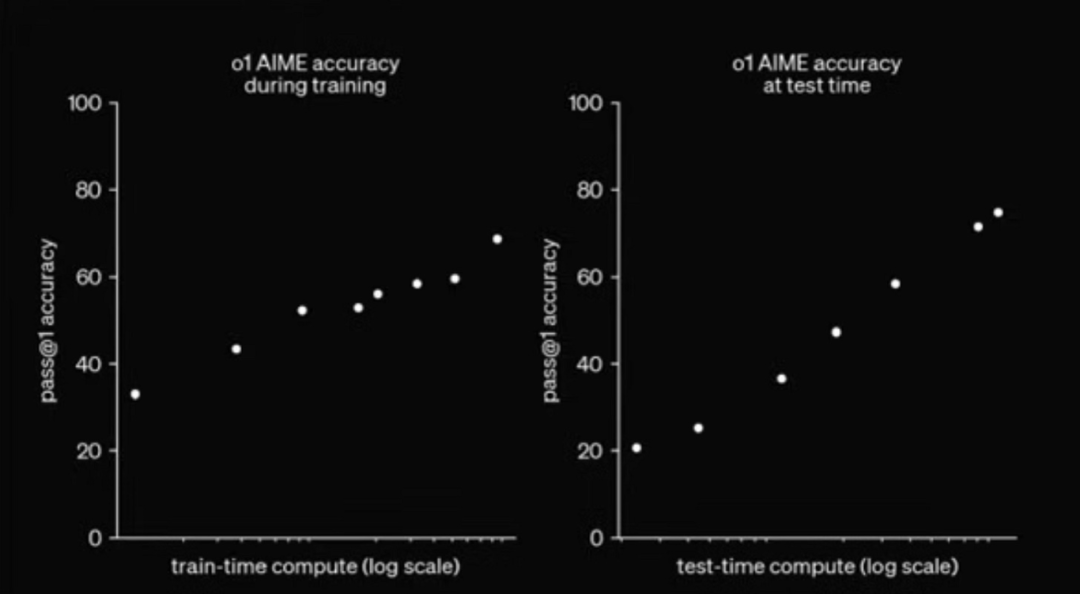image.png

OpenAI 发布的关于 o1 模型测试时计算扩展效果的图示表明：模型的准确率相对于对数尺度的计算量呈现可预测的增长，表明存在指数关系

但像 o1 这类模型背后的实现原理究竟是什么？测试时计算扩展（test-time compute scaling）又有哪些不同的实现机制与技术路径？目前我尚未找到关于此技术直观系统的综述，而 OpenAI 对其技术细节守口如瓶，因此本文将尝试构建一个解读框架。

本篇博客将结合近期的大量文献研究以及与多家实验室机器学习研究者的交流，系统梳理实现测试时计算扩展的主要技术路径。

1.测试时计算的基本实现机制

1.1 N 选 1 采样、多数投票（majority voting）及相关方法

其核心思想是让语言模型在推理阶段生成多个可能的输出，然后通过采样、投票或其他评估/验证器方法来选出最佳答案。这种方法无需改变模型的训练方式，但确实能作为一个有效的基线方案。

Large Language Monkeys[3]

其中的第一点细微差异在于验证器的设计。多数投票（majority voting）等简单方法通用性虽强但效果有限。代码、数学等特定领域可采用专用的验证器（如代码的单元测试与编译器、数学的符号计算引擎），但缺乏普适性。目前的主流趋势是通过微调大语言模型构建专用验证器（参见此案例[4]）。

另一个问题在于，对于许多更复杂的问题，传统的采样方法可能永远无法生成正确答案（或者需要耗费大量计算资源才能以足够高的概率生成正确答案）。后续我们将看到，解决这一问题的正确方法要么基于优质推理轨迹进行训练，要么通过奖励机制引导模型完成复杂推理。

1.2 思维链（Chain of thought）

第二种方法是让语言模型生成极其详细的长链思维推理轨迹，以此提升推理能力。这种方式本质上是单一模型通过自回归方式产生大量 token 的自我对话过程 —— 并不依赖外部系统或控制流程。OpenAI 在其 o1 公告中展示了此类案例[5]。

虽然基础版本可通过提示词工程实现（例如“逐步思考”），但其进阶版本需要专门的预训练与后训练技术，以优化这类长链推理轨迹的生成效果。

这里的关键差异在于模型如何通过训练提升长链推理能力。大致有以下实现路径：

1）监督学习（Supervised learning） —— 理论上可通过大量人工撰写的长链思维样本进行训练。但实践中难以获取足够的高质量数据：公开领域的高水平长篇幅推理样本稀缺，且人工制作成本极高。

2）合成推理轨迹（Synthetic reasoning traces） —— 在特定问题领域，可通过程序化方法生成复杂的推理轨迹。例如这项研究[6]利用知识图谱生成保证正确性的问题/推理/答案三元组。在数学和计算机科学领域，还可使用形式化系统（如符号计算引擎、Lean 语言[7]、编译器与构建系统）产生合成推理链，作为模型的训练样本。

3）采样&验证 —— 要求大语言模型生成多个推理输出，通过验证机制或奖励模型区分优劣推理链，进而构建用于后训练的强化学习数据集。核心区别在于使用结果奖励模型（ORM，验证最终输出的正确性）还是过程奖励模型[8]（PRM，对局部推理链进行奖励评估）。该领域存在非常多的方法：包括采样生成方式、验证器的训练或设计、以及整合奖励信号的强化学习系统架构等。

此处的考量在于：如何在a. 数据规模 b. 计算可行性 c. 人力成本这三个维度实现高效扩展？OpenAI 强调其 o1 技术具备“数据高效特性（data-efficient）”，暗示其很可能深度融合了合成数据与基于强化学习的验证技术，而非某种依赖人工标注的推理数据集。

合成数据技术虽有效，但通常局限于特定领域和更易量化的问题类型，因此其泛化能力仍存疑。

采样技术面临的挑战在于，许多复杂问题的推理搜索空间过大，既无法进行穷举生成，也难以高效验证。这与机器人等强化学习领域面临的问题相似 —— 需要巧妙地模拟或“搜索”结果空间，并设计奖励函数。

这正是过程奖励模型（PRM）的价值核心 —— 它能提前终止错误的推理路径，聚焦于成功概率较高的中间状态进行分支（相关论述参见该论文[9]第 3.3 节）。

关于如何构建推理轨迹结构以提升训练效果，当前存在大量前沿探索：Dualformer[10] 在训练过程中有选择性地遮蔽部分推理轨迹，旨在让模型习得类似人类“系统 1”的心理启发式思维；Stream of Search[11] 研究则发现包含错误回溯、自我修正的“不完美”推理轨迹，相比完美的线性推理更具训练价值；另有论文[12]证实带回溯纠错的错误推理链对训练有益；Beyond A[13] 甚至通过 A* 等经典搜索算法构建训练样本，来教导模型如何进行搜索。

1.3 推理时搜索（及其他辅助系统）

实现推理阶段计算扩展的第三大路径，是在推理过程中实际采用某种搜索技术。这意味着推理不再仅仅是模型推理问题，更演变为系统工程问题 —— 需要引入某种控制流或流程编排机制，而非单纯依赖单一模型的词元输出。

一些有趣的例子表明，这种范式不仅限于“标准”的大语言模型。例如，AlphaZero[14] 通过训练后的神经网络指导蒙特卡洛树搜索算法选择最佳落子位置；AlphaProof[15] 则结合预训练大语言模型与强化学习算法生成候选解决方案，再通过 Lean 证明辅助语言（proof assistant language）进行验证。

当前 LLM 研究中，最常见的实现形式是在推理阶段集成某种“搜索+验证”技术：模型首先生成 N 个候选的推理步骤，经验证器或奖励模型评分筛选后，然后在最优候选子集中重复此过程。值得注意的是，前文讨论的“N 选 1 采样”方法可视为该体系的子集。

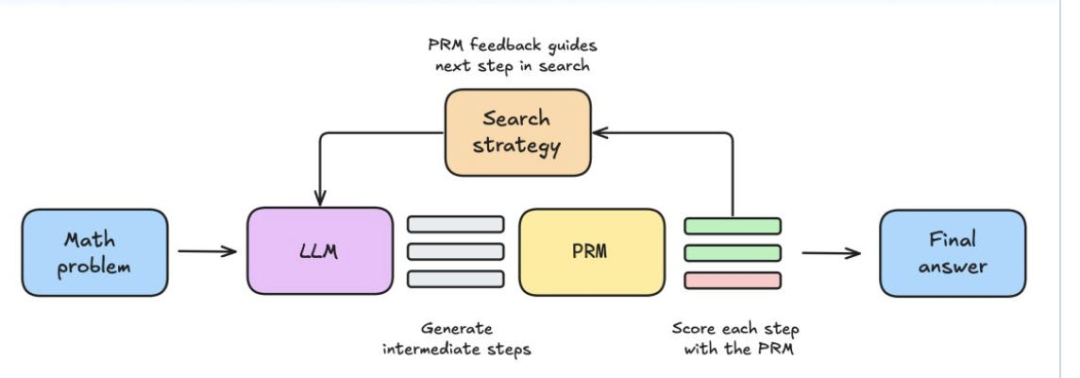HuggingFace 关于通过搜索+过程奖励模型实现测试时计算的综述

该领域的优秀研究案例包括：Tree of Thoughts[16]、Self-Evaluation Guided Beam Search for Reasoning[17] 以及 Reasoning with Language Model is Planning with World Model[18]。这些方法均融合了搜索技术（广度优先搜索、深度优先搜索、波束搜索、蒙特卡洛树搜索）与验证机制来引导语言模型推理生成。LLM Reasoners[19] 论文中的可视化呈现（如下图所示）直观展示了这些技术的运作方式。这些方法在核心思路上高度一致。

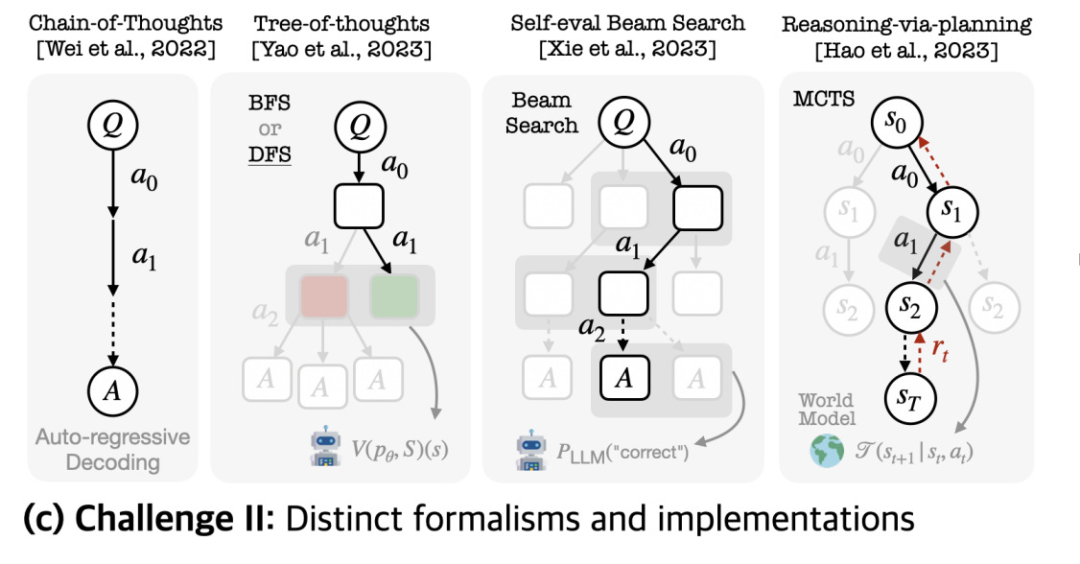image.png

值得注意的是，这种“搜索技术+验证器+生成模型”的组合范式与前文所述的思维链技术几乎同构 —— 唯一区别在于这些技术是离线应用于生成后训练强化学习数据集，还是在推理时在线应用。但两种方式都实现了测试时计算扩展：前者通过训练使模型在测试时进行更长时间的推理，而后者则在推理过程中引导模型生成更大量的输出。

除搜索算法外，还可集成其他类型的辅助系统来增强生成模型。RAP 论文[18]便是一个典型范例：研究者使用一个辅助 LLM 作为“世界模型”来追踪环境状态。换句话说，当生成式 LLM 持续输出回溯、思考、权衡等推理动作时，世界模型会同步跟踪每个动作执行后的“世界状态”。

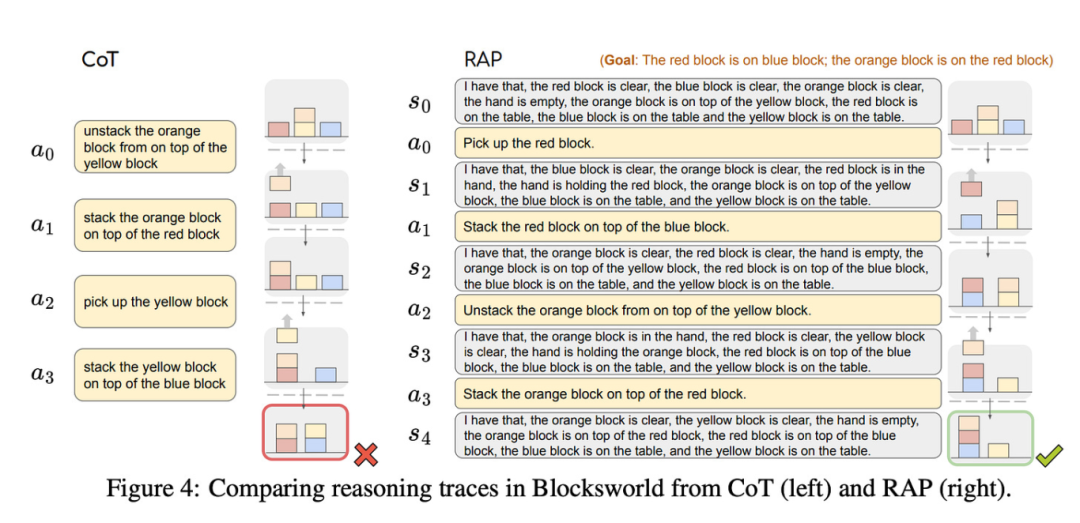image.png

标准思维链动作序列与世界模型方法的可视化对比（后者在每个动作后均保留了“世界状态”）

从理论上讲，这种方式让模型能更轻松地推断后续动作产生的影响。相较于单一思维链的输出，模型必须隐式回放整个动作序列才能理解当前世界状态。

上文提到的推理研究论文[19]提出了一个有趣的形式化框架，试图将多数投票、思维链、搜索技术等不同方法统一到同一个理论体系中。

研究者认为这些技术本质上都是以下三要素的组合：

1）用于确定不同推理步骤优先级的奖励函数

2）用于定义推理状态转换的世界模型

3）用于探索广阔推理空间的搜索算法

在此框架下，标准的思维链推理的奖励函数等同于默认模型似然输出，其世界模型仅简单地将推理动作持续追加到完整动作历史中，并采用始终对输出概率分布进行单次采样的“贪婪”搜索算法。

笔者认为这种分析视角颇具启发性。该论文还通过基准测试发现：搜索技术持续优于思维链推理，而 RAP（世界模型+搜索技术）则始终超越纯搜索方法。

斯坦福大学近期对推理模型的元综述（meta overview）[20]也描述了类似的思维框架 —— 认为这些方法大多都是“生成器、验证器和搜索组件的集成”，这本质上是相同的框架。

2.其他考量因素

2.1 验证器机制

如我们所见，这些技术的效果很大程度上取决于验证器的质量及其验证能力。启发式/自动验证器（Heuristic/automatic verifiers）虽有效但天然具有领域局限性（例如，编程题目中的测试用例）。学习型验证器（Learned verifiers）虽可行，但需要特定领域的高质量训练数据 —— 可参考 OpenAI 这篇早期的论文[21]，他们训练了用于数学问题的学习型验证器。直接使用 LLM 用作验证器虽已取得显著进展，但该方法的可行性仍存在一定局限。基于过程的验证器（Process based verifiers）非常重要，但其实现难度远高于基于结果的验证器（outcome based verifiers）。

MuZero[22] 为此领域的发展提供了一个重要参照 —— 这个无模型的强化学习系统能掌握多种复杂游戏并达到顶尖水平。“无模型（Model-free）”意味着其强化学习算法中并未编码任何特定游戏规则。

这种领域无关的验证器设计似乎对模型在推理能力上实现普遍提升非常重要。当然，关键问题在于，相较于围棋、国际象棋、将棋和 Atari 游戏等奖励函数明确的领域，如何在奖励机制更模糊的领域实现类似效果仍待探索。

2.2 泛化能力存疑

这篇精彩的博文深入探讨了将强化学习应用于推理领域的挑战[23]，特别是在 OpenAI 的 o1 模型这个具体背景下来讨论这个问题。o1 采用强化学习技术，而强化学习在奖励信号清晰且频繁的领域效果最佳，但现实是大多数领域缺乏这种明确的奖励机制。

……

OpenAI 承认 o1 是在易于验证的领域进行训练的，但希望其推理能力能泛化到所有领域。这种跨领域的泛化能力能否实现，是一个价值万亿美元的问题。我先直截了当地说出我的观点：

⚠️ o1 风格的推理模型无法实现超越训练领域的有效泛化

从实际案例来看，当前多数测试时计算模型在特定问题领域（如数学、逻辑、计算机科学）表现突出，但在其他领域并未展现明显优势。许多体验过这类模型的研究者反馈，它们在传统生成任务上的表现反而明显下降。基于强化学习的推理技术能否有效泛化到验证难度更高的领域，仍是一个值得探索的开放性问题。

2.3 词元空间与隐空间中的推理

与上述所有方法形成有趣对照的是：词元空间究竟是否为模型推理的最优方式？现有研究开始探索让模型直接在隐空间[24]中推理 —— 即在推理过程中将隐藏状态反馈给模型，而非解码后的词元。

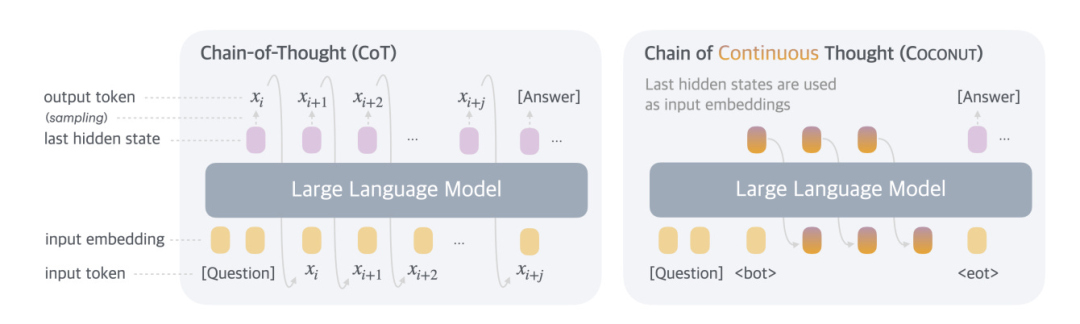image.png

从理论上讲，隐空间推理可能更具优势，因为隐藏状态（hidden state）代表了下一词元生成的概率分布，而词元本质上是该分布的“采样样本”。相较于仅选择一个状态，在所有可能状态下进行推理更接近人类的推理模式，可能有提升效果。

这种方法的潜在缺陷是，此类模型不会向用户“展示推理过程”。但考虑到 OpenAI 等公司已经开始隐藏推理步骤，这个缺点或许无关紧要。理论上仍可可视化词元输出而同时在隐空间推理，但这可能导致用户所见与模型实际推理过程出现偏差。

2.4 智能体推理机制

我特别关注这些技术如何映射到智能体领域。优化模型的多步骤复杂推理轨迹，与优化智能体的多步骤推理轨迹存在高度相似性 —— 唯一区别在于智能体的子步骤被拆分为不同的模型调用，且通常涉及更多动态组件（如函数调用等）。

观察到许多领先的智能体创业公司（如 Cognition、Basis 等）都将这些理念融入其智能体设计。例如，多家智能体公司会采集智能体的运行轨迹，通过搜索技术+奖励模型进行回放来推演反事实推理路径（counterfactual reasoning paths），并将这些反事实轨迹（counterfactual trajectories）作为微调样本用于提升智能体系统性能。

对于需要 50-100+ 次链式 LLM 调用来在复杂工具环境中完成任务的智能体而言，这种方法至关重要 —— 因为单次请求下智能体可执行的动作组合复杂度极高。

特别值得关注的是，相较于在模型层通用地解决多步推理问题，设计针对特定领域的搜索算法和过程奖励模型显然更具可行性。

这恰好印证了前文提及的那篇博客文章的观点：这些技术可能难以实现泛化。复杂推理的强化学习技术在模型提供商层面或许难以泛化，反而会成为垂直领域智能体创业公司的核心护城河 —— 尤其是在需要高度复杂推理的领域（如会计、税务、金融、建筑等）。

预计未来将出现专门支持此类任务的开发工具（类似微调领域的 MosaicML 生态），帮助智能体创业公司更便捷地构建“搜索技术+验证”层，并为特定应用场景生成训练数据集。

文中链接

[1]https://deepmind.google/discover/blog/alphazero-shedding-new-light-on-chess-shogi-and-go/

[2]https://arxiv.org/abs/1611.09940

[3]https://arxiv.org/pdf/2407.21787

[4]https://arxiv.org/pdf/2408.15240

[5]https://openai.com/index/learning-to-reason-with-llms/

[6]https://extrasensoryai.github.io/enki/blog/synthetic-data-cot/

[7]https://lean-lang.org/about/

[8]https://arxiv.org/pdf/2410.08146

[9]https://arxiv.org/pdf/2501.04682

[10]https://arxiv.org/pdf/2410.09918

[11]https://arxiv.org/abs/2404.03683

[12]https://arxiv.org/abs/2408.16293

[13]https://arxiv.org/pdf/2402.14083

[14]https://deepmind.google/discover/blog/alphazero-shedding-new-light-on-chess-shogi-and-go/

[15]https://deepmind.google/discover/blog/ai-solves-imo-problems-at-silver-medal-level/

[16]https://arxiv.org/pdf/2305.10601

[17]https://arxiv.org/pdf/2305.00633

[18]https://arxiv.org/pdf/2305.14992

[19]https://arxiv.org/pdf/2404.05221

[20]https://arxiv.org/pdf/2501.04682

[21]https://arxiv.org/pdf/2110.14168

[22]https://deepmind.google/discover/blog/muzero-mastering-go-chess-shogi-and-atari-without-rules/

[23]https://aidanmclaughlin.notion.site/reasoners-problem

[24]https://arxiv.org/pdf/2412.06769