统一视角下的HPT：动态融合SFT与RL，释放LLM后训练新潜能

大家好，我是肆〇柒。今天探索一篇来自清华大学、上海AI实验室与微信AI团队的前沿研究。这篇论文提出了一种名为HPT的创新算法，它像一位“智能教练”，能根据模型的实时表现，动态决定是该用监督学习“补基础”，还是用强化学习“练推理”，从而解决后训练中SFT与RL难以调和的矛盾，让模型性能实现质的飞跃。

后训练（Post-Training）是决定模型最终战斗力的关键战役。然而，这场战役往往让一线算法工程师们深陷泥潭：是选择高效但死板的监督微调（SFT, Supervised Fine-Tuning），还是选择潜力巨大但极不稳定的强化学习（RL, Reinforcement Learning）？是咬牙上成本高昂的"SFT→RL"两阶段流水线，还是冒险尝试效果飘忽不定的混合策略？

调参的噩梦、效果的瓶颈、资源的浪费，构成了后训练领域挥之不去的痛点。现在，这种名为"混合后训练"（Hybrid Post-Training, HPT）的新算法，正以其简洁、强大和自适应的特性，为这个领域带来一场创新思考。它不再将SFT与RL视为水火不容的对手，而是基于一个深刻的统一理论框架，让两者协同工作，动态互补，最终实现"1+1>2"的效果。

你是否也受困于LLM后训练？

后训练的困境，源于SFT与RL两种范式天然的矛盾与互补。直接对基础模型应用RL（即"Zero RL"），就如同让一个刚学会走路的孩子去参加马拉松——模型缺乏基本能力，采样出的轨迹（Trajectory）质量低下，无法获得有效奖励信号，训练极易崩溃。在Qwen2.5-Math-1.5B上的实验表明，纯GRPO训练50轮后，仍有近30%的问题产生连续滚动错误（如下图所示），这意味着工程师每天要面对数百条"模型已崩溃"的报警，不得不反复重启训练。

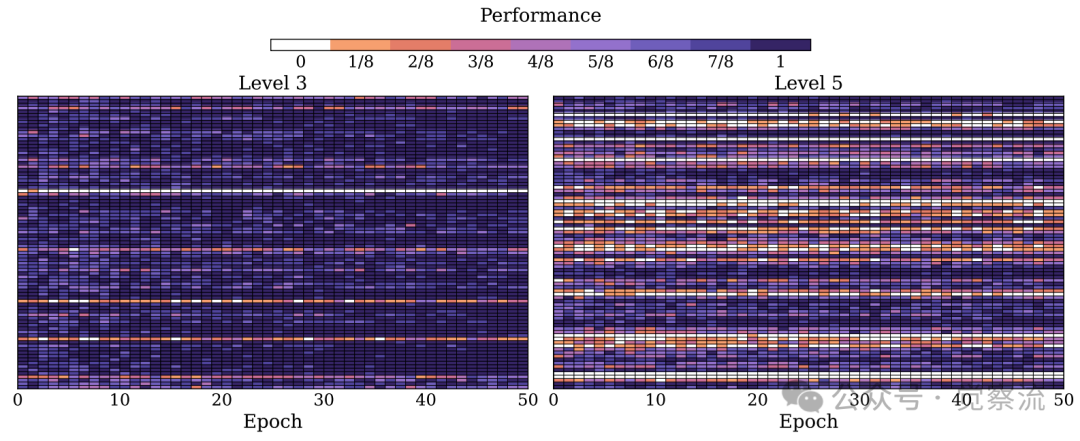
 GRPO training dynamics of SFT→GRPO on Qwen2.5-Math-1.5B across 50 training epochs. GRPO训练动态示意图

反之，纯SFT虽然能让模型快速掌握特定领域的知识，却像给学生喂"标准答案"，模型只会死记硬背，一旦遇到训练数据分布之外（Out-of-Distribution）的问题，便束手无策，泛化能力堪忧。更令人头疼的是，SFT→RL的两阶段流水线虽然看似完美，实则代价高昂：它需要两套独立的训练流程，在8*A800 GPU上额外消耗200+ GPU小时（约$1,200成本），且两个阶段的衔接往往成为新的瓶颈——第一阶段SFT的过拟合，可能会在第二阶段RL中扼杀模型宝贵的探索能力。

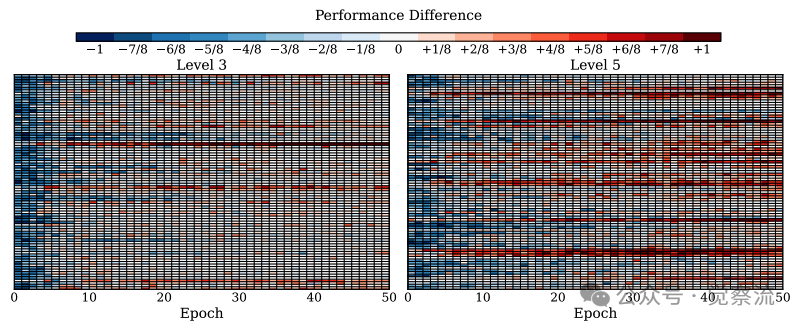
更进一步的解决方案，如LUFFY等混合策略，尝试在单个训练阶段内同时使用SFT和RL的损失。但这类方法通常依赖一个预设的、固定的混合比例，如同给所有学生用同一套教育方式，无法适应模型在训练过程中能力的动态变化，效果自然不稳定。下图直观展示了这种困境：在SFT→GRPO中，模型在Level 5难题上的表现始终难以突破，而HPT却能持续进步。

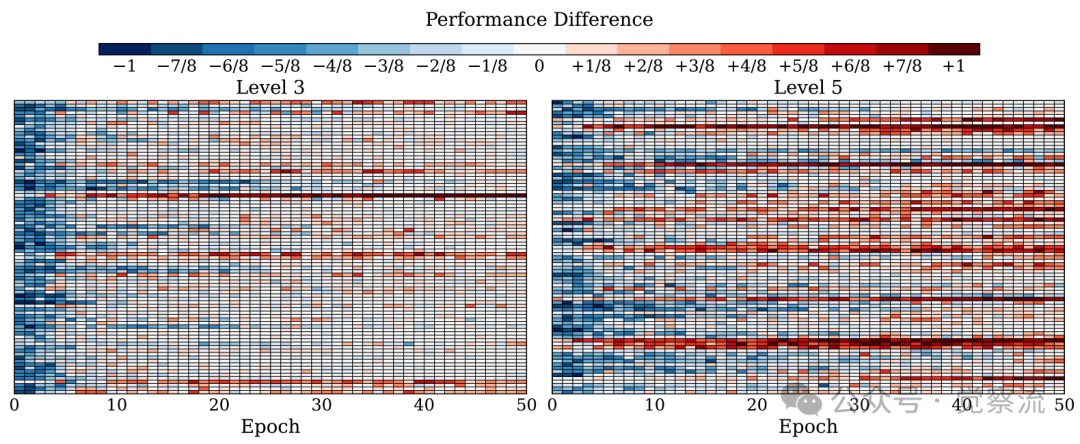
Performance difference(HPT v.s. SFT→GRPO) on Qwen2.5-Math-1.5B across 50 training epochs. HPT与SFT→GRPO性能差异对比

核心问题由此浮现：如何设计一个算法，既能像SFT一样高效地"学得会"，吸收高质量演示数据中的知识，又能像RL一样自由地"想得通"，通过在线探索不断提升泛化和推理能力？HPT算法，正是为解决这一核心矛盾而生。其背后的理论基石，是将SFT和RL统一到一个名为"统一策略梯度估计器"（Unified Policy Gradient Estimator, UPGE）的框架下。

理论基石：共同目标下的梯度统一

HPT的突破性在于，它揭示了SFT与RL并非水火不容，而是优化同一个目标函数的不同路径。论文提出了一个共同优化目标：

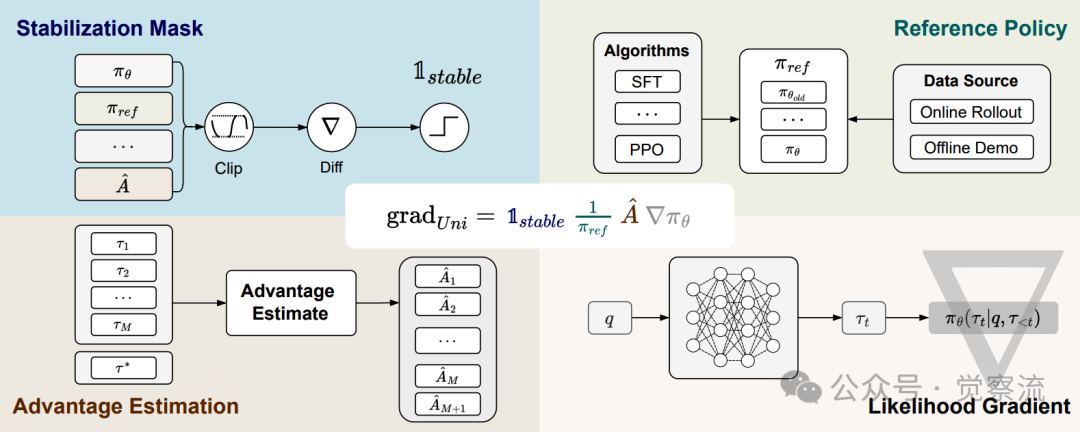统一策略梯度估计器示意图

如上图所示，这个统一公式可拆解为四个可替换的组件：

• 稳定掩码（Stabilization Mask）：决定哪些梯度更新应被保留或屏蔽
• 参考策略分母（Reference Policy）：提供重加权系数，通常为逆概率形式
• 优势估计（Advantage Estimate）：衡量当前响应序列的质量
• 似然梯度（Likelihood Gradient）：将梯度信息从动作映射到模型参数

下表将SFT、PPO、GRPO、LUFFY、SRFT等主流后训练算法的梯度计算，全部映射到这四个组件上。这揭示了一个事实：SFT和GRPO在数学上只差两个开关设置。这意味着工程师不必再纠结"该用SFT还是RL"——就像不必争论"该用铲子还是锄头"，因为HPT自动为你选择最适合当前问题的工具。

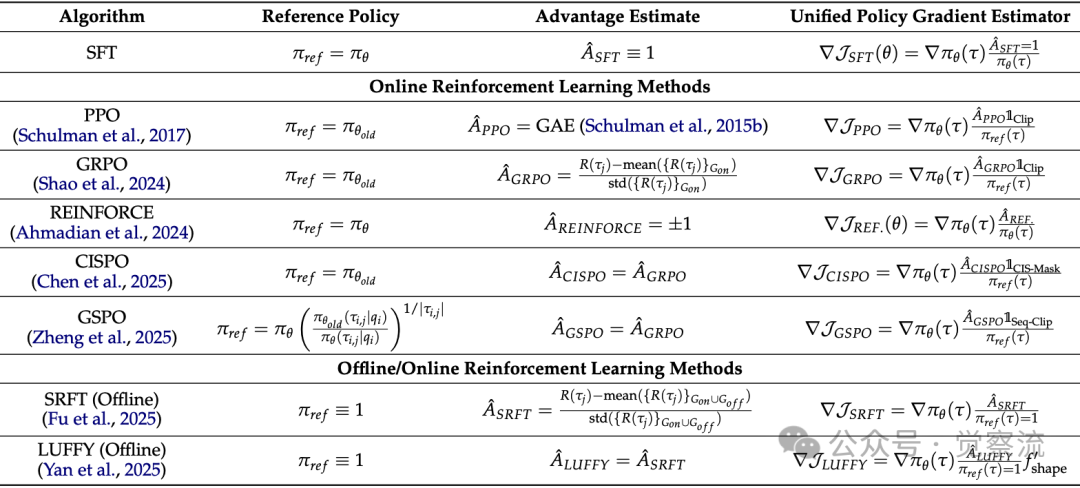
各种后训练算法的理论统一视图

上表展示了不同算法的统一表示，它证明所有后训练算法本质是同一框架的变体。看SFT行：当"参考策略"设为πθ、"优势估计"设为1时，就是传统SFT；看GRPO行：当"参考策略"设为πθold、"优势估计"设为组归一化奖励时，就是当前最火的GRPO。这意味着——SFT和RL不是对立选择，而是同一枚硬币的两面。HPT的突破在于：它不再强迫工程师"二选一"，而是让模型根据当前能力，自动选择最优学习模式。

纯RL的局限性：为什么我们需要SFT

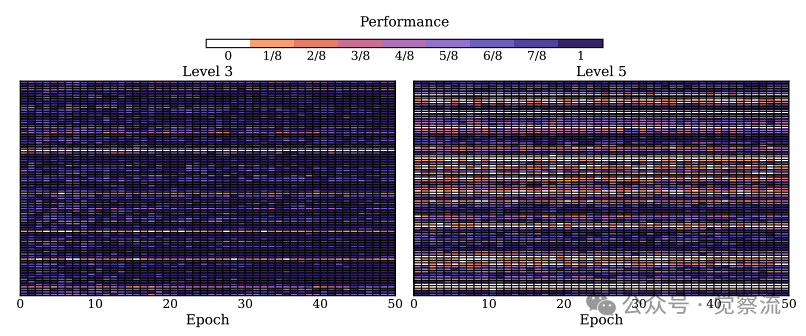
为了更直观地理解SFT的必要性，论文通过上图展示了SFT→GRPO在Qwen2.5-Math-1.5B上的训练动态。研究者选取了85道Level 3（较易）和85道Level 5（最难）的问题进行50轮训练，跟踪每个问题的采样准确率。图中密集的白色区域（甚至连续的白线）表明RL方法在输出中频繁出现滚动错误，这正是纯RL方法的核心局限：当所有输出都频繁出错时，模型难以有效学习。

下图则进一步揭示了HPT如何解决这一问题。该图展示了HPT与SFT→GRPO的性能差异，红色表示HPT表现更好，蓝色表示SFT→GRPO更优。虽然SFT→GRPO前期因已包含SFT阶段而具有优势（蓝色区域），但在训练后期，HPT逐渐超越并最终占据主导（红色区域），特别是在Level 5难题上优势更为明显。这表明HPT通过基于问题级滚动表现的反馈，特别有利于学习更具挑战性的问题。

混合后训练（HPT）算法

UPGE框架的创新意义，不仅在于它统一了数学形式，更在于它揭示了不同算法的本质是在不同数据分布和稳定性假设下对同一目标的梯度估计。既然SFT和RL的梯度都是对"真实梯度"的一种有偏或无偏估计，那么最优的训练策略就不是固定使用某一种估计器，而是应该根据当前模型的状态，动态选择方差最小、偏差最低的那个估计器。

HPT的核心思想可以浓缩为一句话："会的题用RL练推理，不会的题用SFT学答案"。但这一表述背后，蕴含着深刻的动态反馈机制，远非简单的静态分类。

HPT工作流程

HPT的工作流程（如算法伪代码下图所示）是一个闭环的动态反馈系统。

这个算法关键在于基于模型当前表现的实时决策： 

这里的关键是，HPT的决策是实时的、基于模型当前策略的。它不是预先知道哪些题"难"，而是通过让模型对同一个问题进行多次采样，根据其当前表现来决定教学方法。这意味着：

动态门限的科学选择 

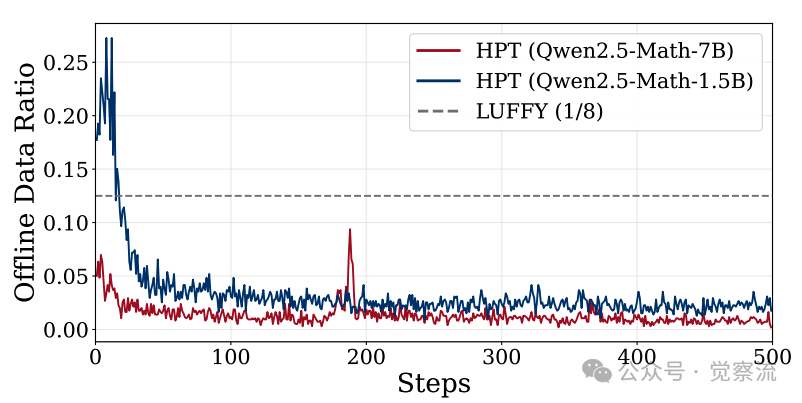
训练过程中动态离线数据比例变化

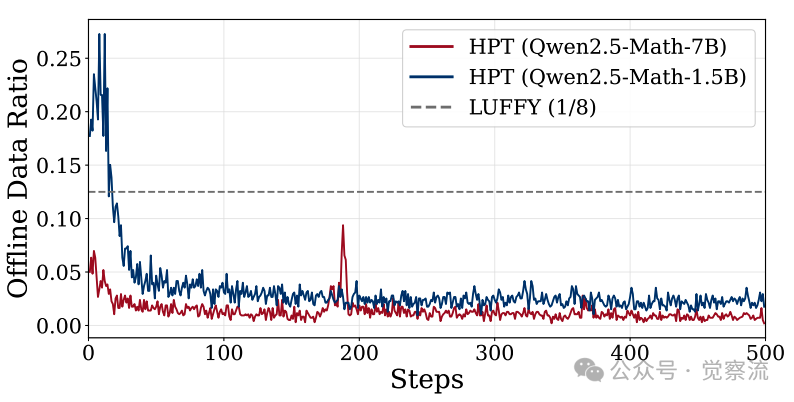
上图清晰地展示了这一过程：训练初期，弱模型（1.5B）的SFT比例高达80%，这是在"补基础"；随着能力提升，比例稳步下降至20%左右，转向"练推理"。而强模型（7B）的下降速度更快，体现了"因材施教"的智能。值得注意的是，较弱的1.5B模型在SFT主导阶段停留的时间比7B模型更长，这与"因材施教"的理论完全吻合。

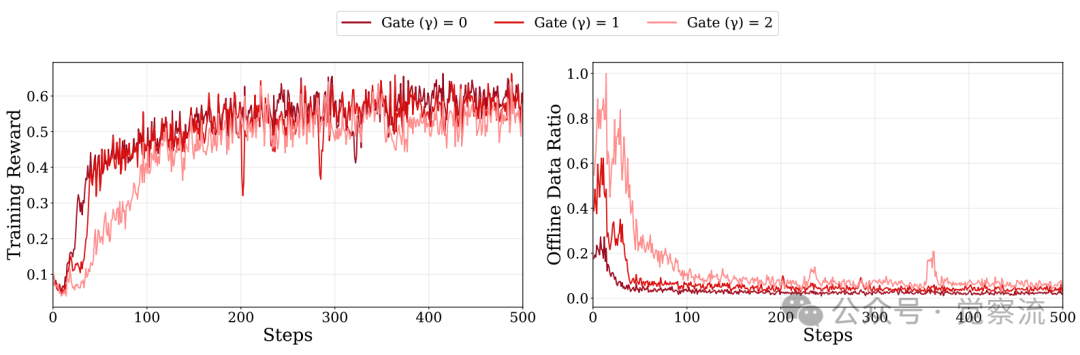
不同门限设置下的训练奖励和离线数据比例对比

上图进一步证实了这一点：虽然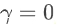的设置在初期SFT比例最低，但其训练奖励的上升速度最快，最终收敛到最高水平。这证明了"少即是多"——对于强模型，过早或过多地介入SFT，反而会打断其宝贵的自主探索过程，将其拉回"死记硬背"的模式。让强模型在探索中犯错，比强行灌输标准答案更能激发其潜力。

HPT到底有多强？

理论的优美，最终需要实践的检验。HPT在多个维度的实测中，都交出了一份令人信服的答卷，其优势不仅体现在最终分数上，更体现在模型能力的本质提升上。

精确的性能对比

在Qwen2.5-Math-7B上，HPT展现了"横扫千军"的统治力。如下表所示，它不仅大幅超越了单一的SFT和GRPO基线，更以显著优势碾压了当前主流的先进方法。在AIME 2024基准上，HPT以33.0分的成绩，领先其最强基线SFT→GRPO（25.7分）7.3个百分点；相较于混合策略LUFFY（26.1分）和SRFT（18.4分），HPT的优势同样明显。这一结果有力地证明了，动态融合的策略远胜于静态的、手工调优的方案。

HPT的强大并非大模型的专属。在参数规模更小、能力相对较弱的Qwen2.5-Math-1.5B和LLaMA3.1-8B模型上，HPT同样带来了显著且稳定的性能增益（见表3）。这表明HPT具有强大的普适性，能够有效提升不同规模、不同架构模型的后训练效果，为资源有限的团队提供了极具性价比的解决方案。

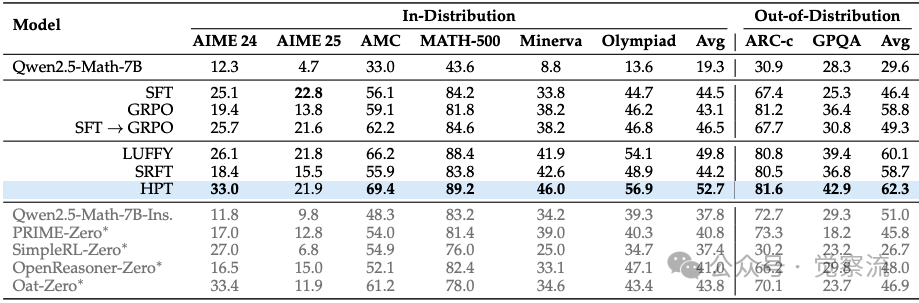
Pass@k与独有解的发现

HPT的强大，不仅体现在最终分数上，更体现在它对模型"能力天花板"的突破。

HPT与基线的Pass@k性能对比

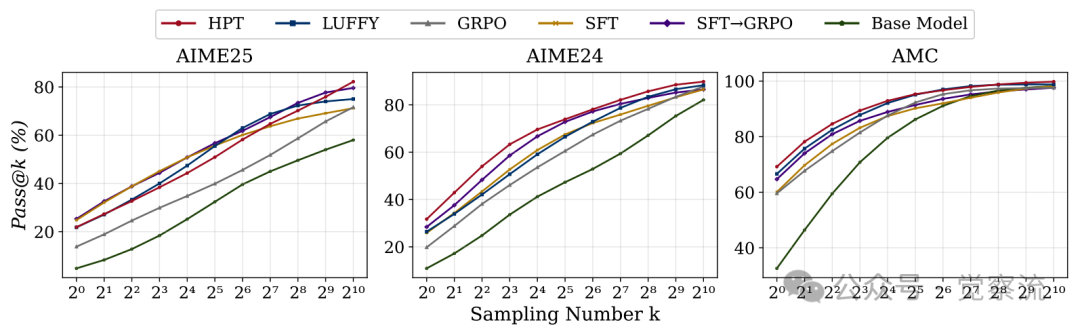
上图是一个极具说服力的证据。图中，纯RL方法（GRPO）的Pass@1024曲线最低，这印证了业界的普遍认知：RL擅长优化已知路径，但难以扩展能力边界。而纯SFT的曲线虽高，却牺牲了推理的灵活性。HPT的曲线则"后来居上"，在高采样数下反超所有基线，稳居第一。

这颠覆了业界认知：HPT不仅Pass@1领先，其Pass@1024（衡量模型极限能力）也全面碾压基线。这意味着——HPT训练的模型在大量尝试中找到正确答案的能力更强。具体看AIME24：当采样1024次时，HPT解题率比GRPO高15%，相当于'原本100道题只能解30道，现在能解45道'。更惊人的是，HPT的曲线始终在最上方，证明它既学到了SFT的知识注入，又保留了RL的探索能力——这才是真正的能力上限突破。

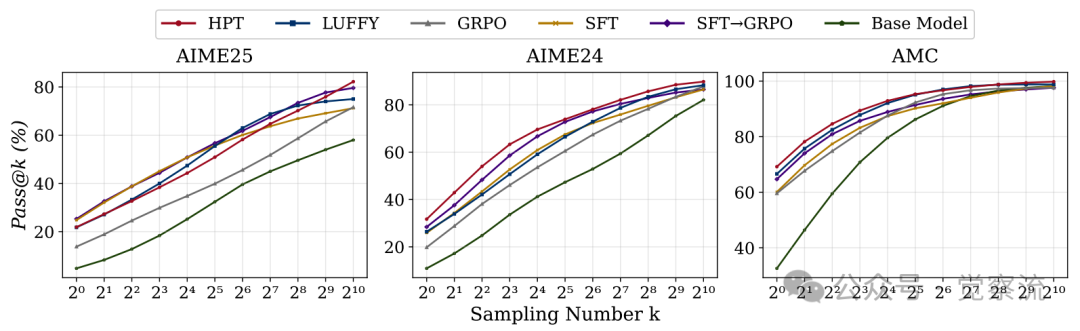
这种能力在攻克难题时表现得淋漓尽致。

MATH-500上独有解的双向分析

上表的'+27/-8'是HPT的'杀手锏'：它多解出27道Level 5奥数难题，仅"遗忘"8道已会题目。这意味着——HPT在攻坚最难问题时，几乎不损失已有能力。对工程师而言，这解决了后训练的终极矛盾：既要探索新能力，又不能忘记旧知识。当你的模型需要同时处理100种复杂任务时，HPT就是那个'不忘本'的智能体。

更令人振奋的是，HPT不仅提升了模型的"做题"能力（Pass@1），更大幅拓展了其"思考"的边界。通过分析模型在大量采样下的表现（Pass@k），研究发现，HPT训练的模型在Pass@1024指标上取得了最高分（见下图）。

HPT与基线的Pass@k性能对比

这一发现极具反直觉性：虽然直观上认为HPT（混合方法）的Pass@k应介于纯SFT和纯GRPO之间，但上图显示，HPT的曲线始终在最上方。这意味着HPT在利用SFT为模型注入新知识的同时，最大程度地保护并增强了模型自主探索、发现新解法的能力，真正提升了模型的能力上限，而非简单的过拟合。这一发现直接回应了业界关于"RL是否能扩展模型能力边界"的讨论，证明了HPT在探索能力上的卓越表现。

验证性能与训练动态

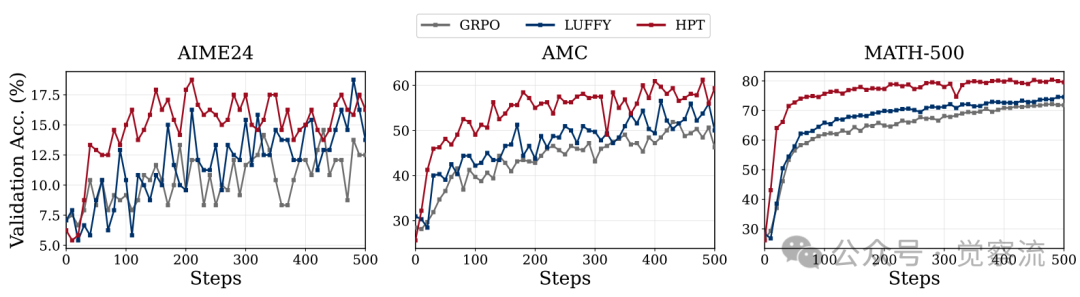
为了进一步验证HPT的稳定性和泛化能力，研究者在Qwen2.5-Math-1.5B上进行了详细的验证性能测试。

Qwen2.5-Math-1.5B在多个基准测试上的验证性能对比

上图展示了HPT在AIME24、AMC和MATH-500等多个基准测试上的验证性能。HPT不仅在训练集上表现优异，在验证集上也持续优于基线方法，且表现稳定。这一结果证实了HPT避免了过拟合风险，能够有效泛化到新问题。

此外，研究者还评估了不同训练范式对Off-policy RL的影响，结果如下表所示：

实验表明，SFT/ON（即HPT）取得了最佳平均性能（41.9分），优于Mix/ON（40.3分）和OFF/ON（38.1分）。这说明对于HPT而言，Off-policy RL可能并非必需，因为SFT已经有效地作为学习离线数据的训练方法。这一发现简化了HPT的实现，避免了复杂的Off-policy RL机制。

如何用好HPT？

对于希望将HPT落地的工程师而言，其配置出人意料地简洁，核心在于理解其动态本质并遵循实验得出的最佳实践。

超参设置：动态平衡的艺术

训练动态可视化：洞悉模型"心路历程"

离线数据比例动态变化：

训练过程中动态离线数据比例变化

上图清晰地展示了HPT的"自适应学习"过程：训练初期，弱模型（1.5B）的SFT比例高达80%，这是在"补基础"；随着能力提升，比例稳步下降至20%左右，转向"练推理"。而强模型（7B）的下降速度更快，体现了"因材施教"的智能。这一动态变化过程是健康且符合预期的。值得注意的是，较弱的1.5B模型在SFT主导阶段停留的时间比7B模型更长，这与"因材施教"的理论完全吻合。

训练熵与响应长度：

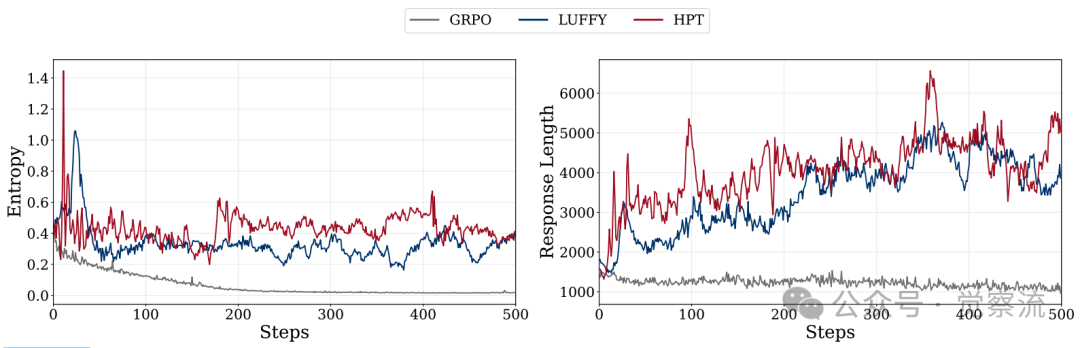
对于一线工程师而言，监控训练过程中的**熵（Entropy）和响应长度（Response Length）**是判断模型是否"学歪了"的关键。

不同方法的训练动态对比

上图显示，HPT能维持比纯RL更高的输出熵。在实践中，这意味着模型的回答更加多样化，没有陷入"只会输出某一种固定模板"的模式崩溃。更关键的是响应长度：HPT模型的响应长度在早期快速攀升后，在RL阶段并未回退。这表明模型已将长推理模式"内化"为自身策略的一部分，而非简单地"背答案"。如果在你的训练中发现响应长度在RL阶段急剧缩短，那很可能意味着RL正在"抹除"SFT阶段学到的复杂推理模式，这是一个危险的信号。

与LUFFY的核心区别

LUFFY等方法是"固定菜谱"，在一个批次内按固定比例混合SFT和RL数据。而HPT是"智能点餐"，它根据模型对每个具体问题的实时表现，动态决定是"学标准答案"还是"练推理过程"。这种细粒度的、基于性能反馈的自适应机制，是HPT效果更优、更稳定的根源。下图直观地展示了不同值下，SFT比例的动态变化过程，越大，SFT介入越频繁。

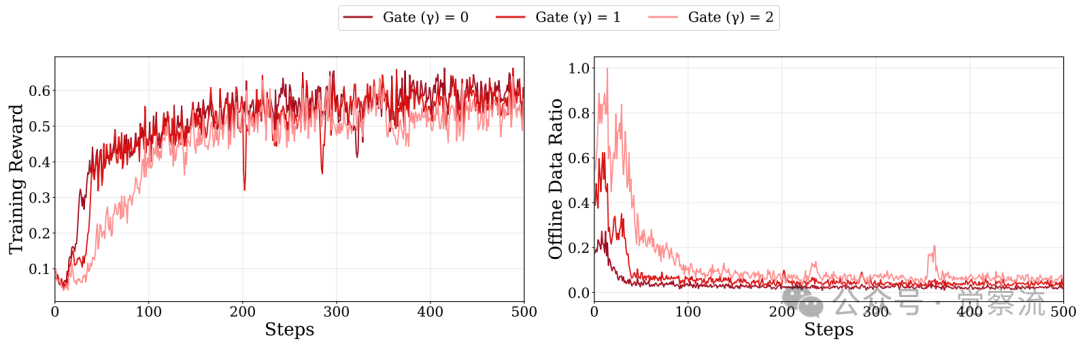
在Qwen2.5-Math-1.5B上，不同门控设置下的训练奖励（左）与离线数据比例（右）对比。

上图显示了HPT的因材施教智慧：对Qwen强模型（γ=0），它几乎全程用RL训练（离线数据比例<20%），因为强模型需要更多探索；对LLaMA弱模型（γ=2），它前期大量用SFT打基础（离线数据比例>60%）。Table 6的消融实验更证明：对Qwen2.5-Math-1.5B，γ=0的效果（41.9分）比γ=2（39.0分）高2.9分——盲目增加SFT比例反而会损害性能。这就像教学生：对学霸，让他多做难题；对学渣，先夯实基础。HPT的智能正在于此。

总结：HPT—后训练的"自动驾驶"模式

HPT 成功地将工程师从繁琐的手动阶段划分、痛苦的比例调优中解放出来，用一个简洁、自适应的算法，无缝融合了SFT的高效与RL的探索潜力。

从实践角度看，HPT效果更强、更稳定、更省心。它在多个模型和基准测试上均取得了顶尖或接近顶尖的结果，无论是大模型还是小模型，都能从中受益。对于一线工程师而言，这意味着更低的试错成本和更高的产出效率。

从方法论上看，HPT的成功是"第一性原理"思维的胜利。它没有在工程技巧的层面修修补补，而是回归到"我们究竟想优化什么？"这个根本问题，从统一的理论框架出发，推导出最优的算法设计。当我们将SFT和RL视为优化同一目标的不同梯度估计器时，一个基于简单性能反馈的门控机制，就能激发出远超复杂手工设计的威力。

HPT的真正价值，是为未来的LLM后训练研究提供了一个强大的范式：当面临看似矛盾的技术路线时，应回到它们共同的优化目标，寻找统一的理论解释，再据此设计自适应的融合算法。HPT不仅是工程实践的胜利，更是统一理论框架指导下算法设计的典范。

告别繁琐的手动阶段划分和比例调整，HPT让一个算法自适应地融合SFT和RL的优势。它不再需要工程师在"SFT"与"RL"之间做非此即彼的选择，而是让模型根据自身能力动态选择最优的学习路径。效果更强、更稳定、更省心，在多个模型和基准测试上均取得SOTA或接近SOTA的结果。

HPT，理应成为每一位LLM后训练工程师工具箱中的新标配。它不仅是一个算法，更是一种"自动驾驶"式的后训练新范式，让模型能够根据自身状态智能地选择最优的学习路径，从而实现能力的最大化提升。