「许多博士(包括过去的我)都陷入了这样一个误区:认为只有在顶级会议上发表论文才是终极目标。」AI 云服务商 Hyperbolic CEO Yuchen Jin 如是说。
但现在,发表论文并不与学术影响力直接画等号了。

Keller Jordan,OpenAI 深度学习团队主要成员之一,用一篇博客就撬开了 OpenAI 的大门。
这篇名为《Muon: An optimizer for hidden layers in neural networks》的博客发布于 2024 年 12 月,而 Keller Jordan 入职 OpenAI 的时间恰好也在此时。
在这篇博客中,Keller Jordan 提出并构建了一种用于神经网络隐藏层的优化器 Muon,其能够在保证神经网络(包括 Transformer 和 CNN)的准确度的前提上大幅提升其训练速度。
为何只发了博客,而不是发表一篇正式的 arXiv 论文,Keller Jordan 这样解释:能否发表一篇关于新优化器的论文,且包含大量看起来不错的结果,和这个优化器是否真的有效之间没有任何联系。「我只相信速通。」
一直以来,研究界的衡量标准过度局限于论文发表,而 Keller Jordan 的案例告诉我们,如果你足够优秀,一篇博客也能打开顶级 AI 科研机构的大门,甚至是 OpenAI。从中,我们也可以看出,OpenAI 在人才招揽方面更注重能力而非其他外在条件。
接下来,我们看看这篇博客内容。
注意,这篇博客发表于 2024 年 12 月 8 日,因此其中对前沿指标的描述可能会略有过时,比如 NanoGPT 速通结果就已经被多次刷新了,下面展示了 Keller Jordan 托管的 NanoGPT 速通的最新八条世界记录,其中最新记录是今年 5 月 25 日创造的,已达到惊人的 2.979 分钟!当然,如此成绩不只靠 Muon,还有 FlexAttention、嵌入优化、架构优化等诸多改进。
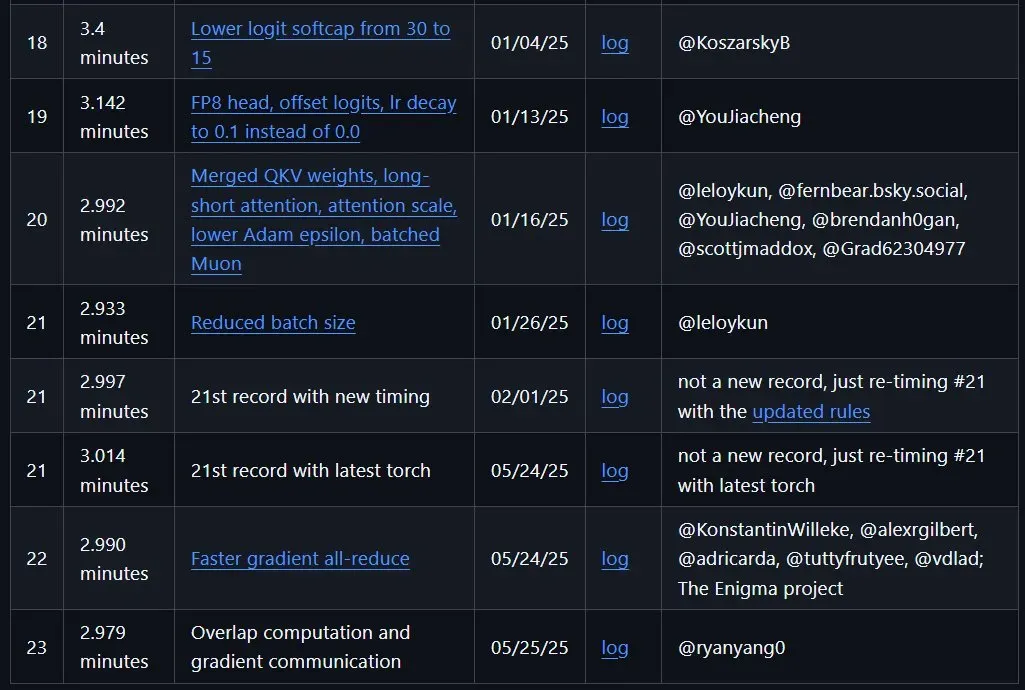
https://github.com/KellerJordan/modded-nanogpt

- 原文地址:https://kellerjordan.github.io/posts/muon/
- Muon 的 PyTorch 实现:https://github.com/KellerJordan/Muon
Muon:一种用于神经网络隐藏层的优化器
Muon 是一种用于神经网络隐藏层的优化器,可用于快速运行 NanoGPT 和 CIFAR-10,并创造了当前最快的训练速度纪录。
目前,人们已经发布了很多使用 Muon 的实证研究结果,所以本文将主要关注 Muon 的设计。
首先,本文将定义 Muon,并概述其迄今为止取得的实证结果;然后将详细讨论其设计,包括与先前研究的联系以及我们对其工作原理的最佳理解;最后将讨论优化研究中的证据标准。
定义
Muon 是一款用户神经网络隐藏层的 2D 参数的优化器。其定义如下:

其中,NewtonSchulz5 定义为以下牛顿 - 舒尔茨矩阵迭代:
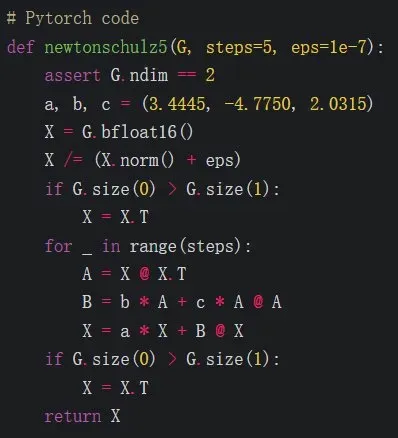
使用 Muon 训练神经网络时,应使用 AdamW 等标准方法优化网络的标量和向量参数以及输入层和输出层。Muon 可用于处理 4D 卷积参数,方法是将其最后三个维度展平(如下所示)。
结果
Muon 已取得以下实证结果:
- 在 CIFAR-10 数据集上,在保证 94% 准确度的前提下,基于 A100 GPU,将训练速度记录从 3.3 秒提升至 2.6 秒。
- 在 FineWeb(一项被称为 NanoGPT 竞速的竞赛任务)上的训练速度记录提升至 3.28 验证损失,提升了 1.35 倍。
- 在扩展到 774M 个参数和 1.5B 亿个参数时,继续表现出了训练速度的提升。
- 在 HellaSwag 上用 10 个 8xH100 小时将一个 1.5B 参数的 Transformer 训练到 GPT-2 XL 级别性能。而使用 AdamW 达到相同结果需要 13.3 小时。
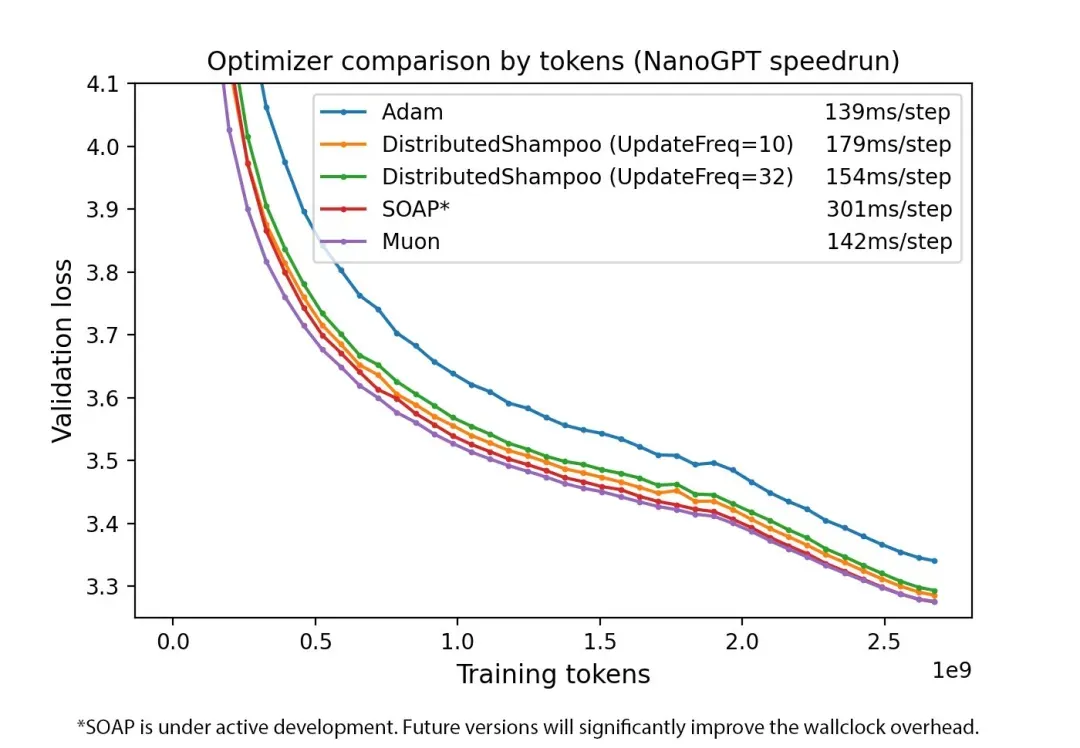
图 1. 按样本效率比较优化器。
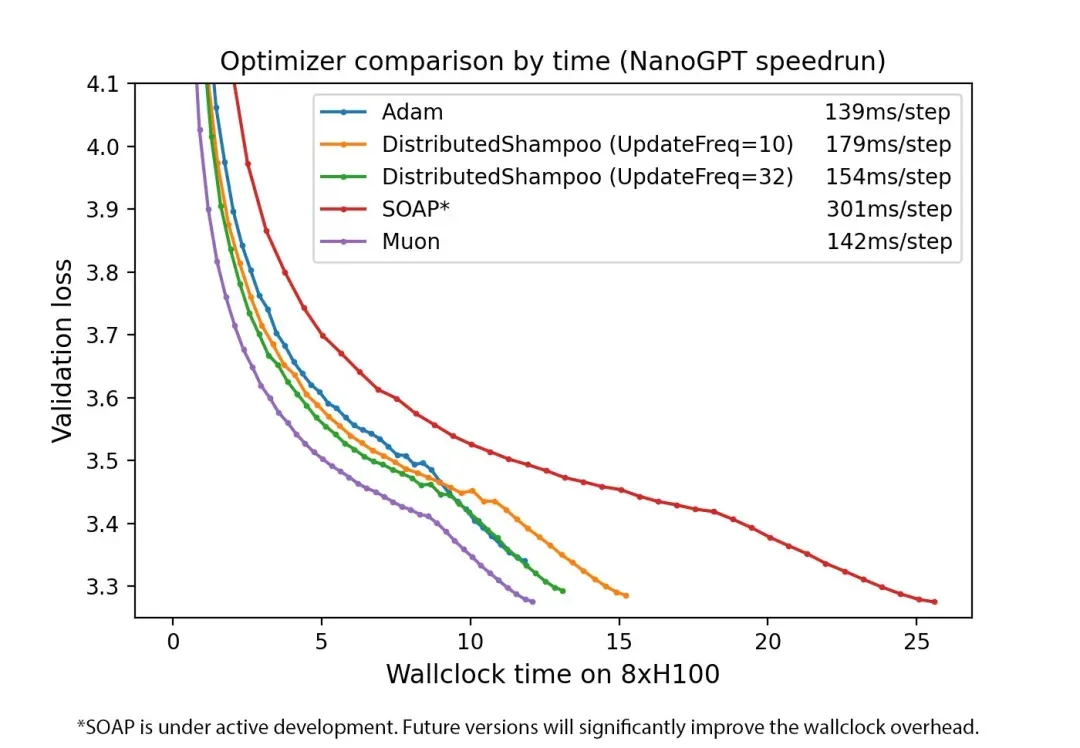
图 2. 按时间比较优化器。
此外,以下是 Muon 和 AdamW 在训练 1.5B 参数语言模型时的比较。两个优化器均已经过微调。
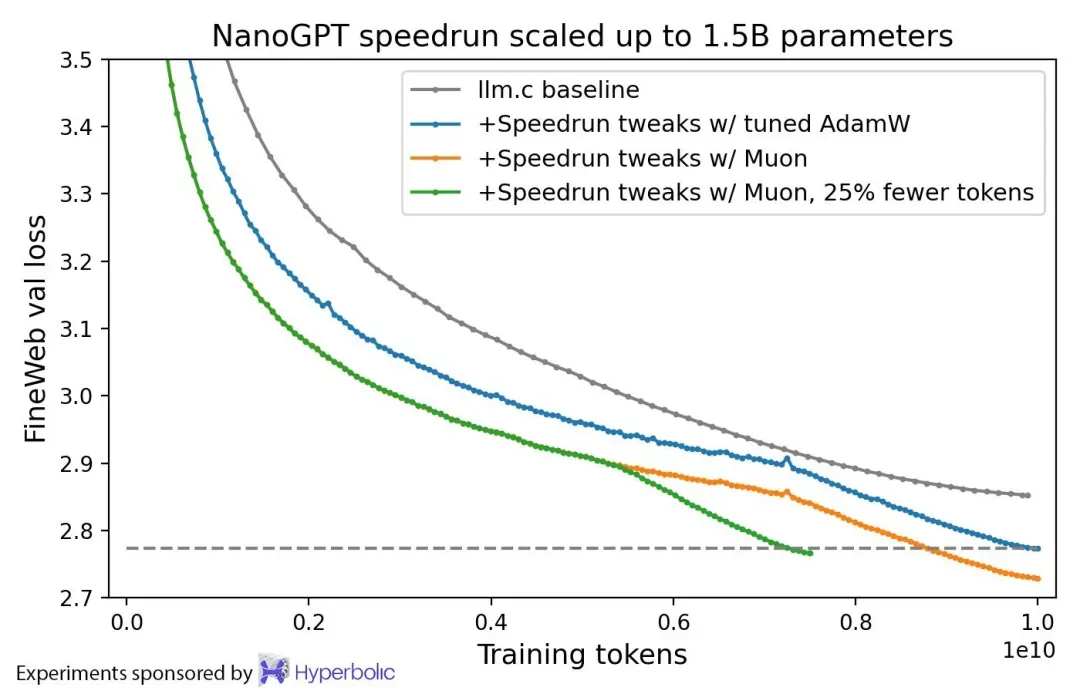
图 3. Muon 与 AdamW 在 1.5B 短训练上的比较。
Muon 的设计
Muon,全称 MomentUm Orthogonalized by Newton-Schulz,其优化 2D 神经网络参数的方式是:获取 SGD - 动量生成的更新,对每个更新应用 Newton-Schulz (NS) 迭代作为后处理步骤,然后在将更新应用于参数。
NS 迭代的作用是近似正交化更新矩阵,即应用以下运算:
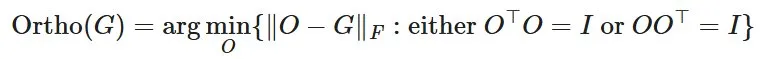
也就是说,NS 迭代实际上会将 SGD - 动量的更新矩阵替换为与其最接近的半正交矩阵。这相当于用 UVᵀ 替换更新,其中 USVᵀ 是其奇异值分解 (SVD)。
为什么正交化更新是有益的?
我们首先想指出一个有效的答案是:这样就没问题了吗?
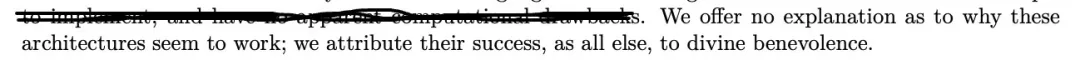
但是,对于源自 Bernstein & Newhouse (2024) 对 Shampoo (Gupta et al. 2018) 分析的理论动机,请参阅后文。
而在实验验证中,我们基于人工检查观察到,SGD - 动量和 Adam 对基于 Transformer 的神经网络中的 2D 参数产生的更新通常具有非常高的条件数。也就是说,它们几乎都是低秩矩阵,所有神经元的更新仅由少数几个方向主导。我们推测,正交化会有效地增加了其他「稀有方向」的规模,这些方向在更新中幅度很小,但对学习仍然很重要。
消除 NS 迭代的替代方案
除了 NS 迭代之外,还有其他几种矩阵正交化的选项。本小节将解释为什么没有使用其中两种方法。请参阅 Bernstein & Newhouse (2024) 的附录 A,获取更完整的可用方法列表。
SVD(即计算更新的 USVᵀ 分解,然后用 UVᵀ 替换更新)易于理解,但我们不使用它,因为它太慢了。
耦合牛顿迭代法 (Coupled Newton iteration) 曾在 Shampoo 的实现中被用于执行逆四次方根,并且可以被轻松地调整用于执行正交化。但我们没有使用它,因为我们发现它必须至少以 float32 精度运行才能避免数值不稳定,而这会导致它在现代 GPU 上运行缓慢。
相比之下,我们发现牛顿 - 舒尔茨迭代可以在 bfloat16 精度下稳定运行。因此,我们选择它们作为正交化更新的首选方法。
证明 NS 迭代能够让更新正交化
为了理解 NS 迭代使更新正交化的原因,令 G=USVᵀ 为 SGD - 动量生成的更新矩阵的 SVD。然后,对系数 (a,b,c) 运行一步 NS 迭代,输出结果如下:
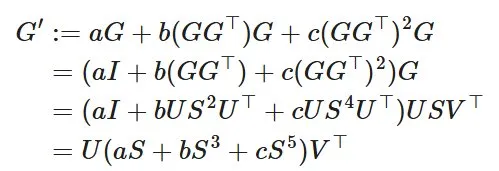
一般来说,如果定义五次多项式 φ(x)=ax+bx³+cx⁵,那么对系数 (a,b,c) 进行 N 步 NS 迭代会输出结果 Uφᴺ(S) Vᵀ,其中 φᴺ(S) 表示对构成 S 对角线的奇异值 N 次逐元素应用 φ。
因此,为了保证 NS 迭代收敛于 Ortho (G)=UVᵀ,需要做的就是 (1) 确保 S 的初始元素在 [0,1] 范围内;(2) 选择系数,使得当 N→∞ 时,φᴺ(x)→1。
为了满足第一个条件,只需在开始 NS 迭代之前将 G 替换为 G/‖G‖F。这种重新缩放是有益的,因为 Ortho (cG)=Ortho (G)。
为了满足当 N→∞ 时 φᴺ(x)→1,会有一定的自由度,因为 (a,b,c) 有很多符合此性质的可能选择。稍后我们将优化这个选择,但现在可在下图中看到,简单的基线 (a,b,c)=(2,−1.5,0.5) 已经有效。
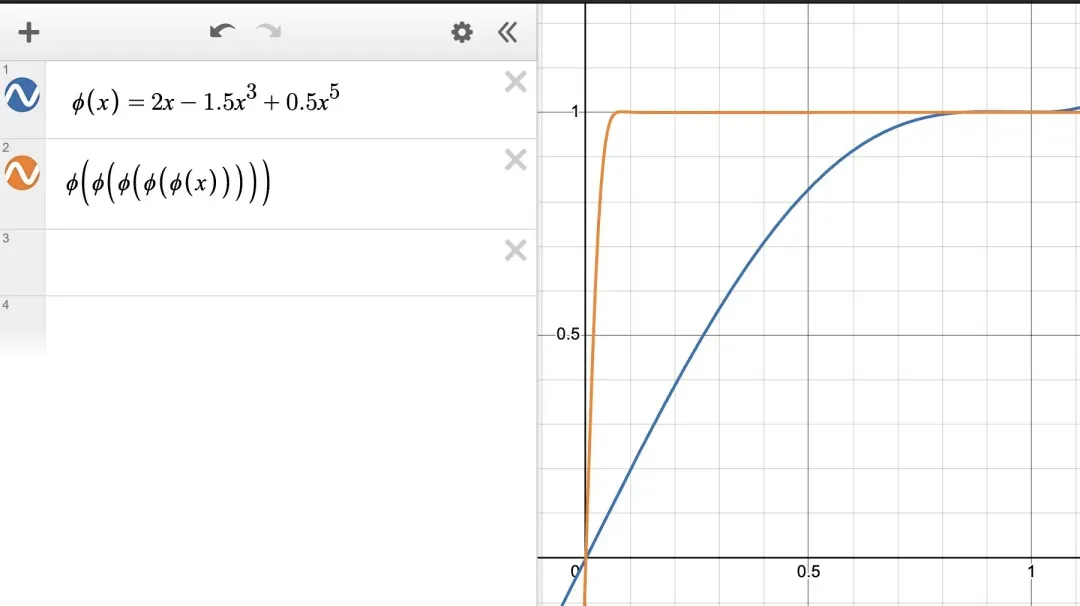
图 4. 牛顿 - 舒尔茨迭代的基线系数。
调整系数
虽然 NS 系数 (a,b,c)=(2,−1.5,0.5) 已经能够完美地实现更新的正交化,但我们可以进一步调整它们,以减少需要运行的 NS 迭代步数。
- 我们希望 a 尽可能大,因为 φ′(0)=a 意味着该系数控制着初始奇异值较小时的收敛速度。
- 对于每个 x∈[0,1],我们希望 φᴺ(x) 在 N→∞ 时收敛到 [1−ε,1+ε] 范围内的一个值,使得 NS 迭代的结果与 Ortho (G) 相差不大。
这里有一个令人惊讶的观察结果:根据实际经验,ε 可以高达 0.3 左右,而不会损害基于 Muon 的训练的损失曲线。因此,我们的目标是最大化 a,使
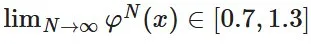
有很多方法可以解决这个约束优化问题。而这里使用一种基于梯度的临时方法,最终得到系数 (3.4445,4.7750,2.0315),这也是最终设计 Muon 时所使用的稀疏。这些系数的变化如下图所示。请注意 x=0 附近的陡然增长。
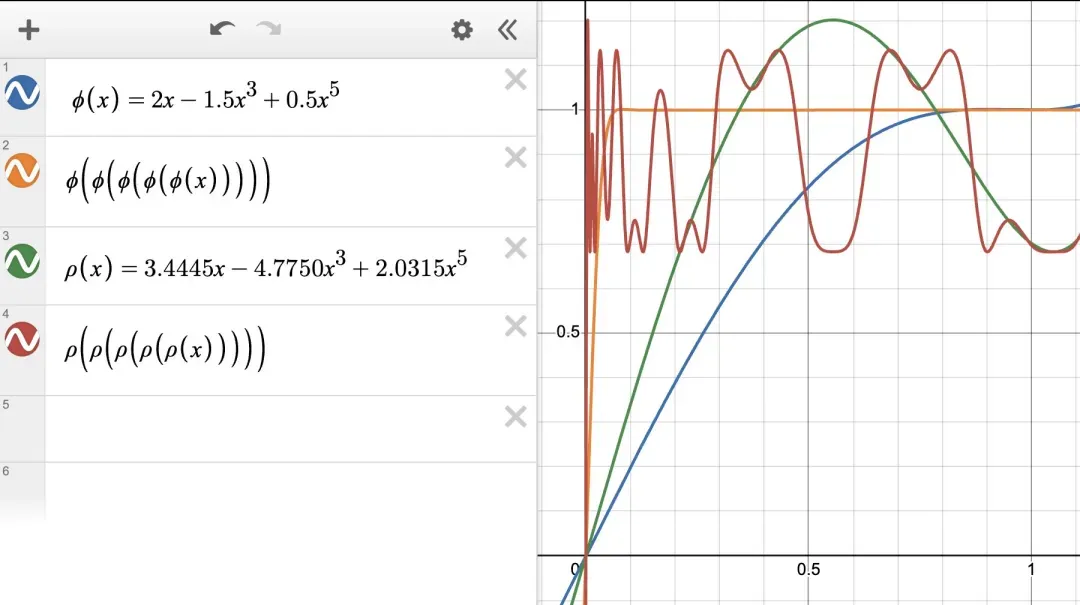
图 5. 调整后的牛顿 - 舒尔茨迭代系数。
在我们的实验中,当使用这些系数的 Muon 来训练 Transformer 语言模型和小型卷积网络时,只需运行 5 步 NS 迭代即可。
我们也考虑过使用三阶和七阶多项式来进行 NS 迭代,但发现这些方法无法进一步改善时间开销。
运行时分析
本节将分析 Muon 的运行时和内存需求。
在应用 NS 迭代之前,Muon 只是标准的 SGD 动量,因此其内存需求相同。
对于网络中的每个 n×m 矩阵参数(例如,设 m≤n),NS 迭代的每一步都需要 2 (2nm²+m³) 个矩阵乘法 FLOP,对于平方参数,最多为 6nm²。因此,与 SGD 相比,Muon 所需的额外 FLOP 最多为 6Tnm²,其中 T 是 NS 迭代次数(通常我们取 T=5)。
如果该参数参数化了一个线性层,那么执行一个训练步骤(即前向和后向传递)所需的 FLOP 基准量为 6nm²,其中 B 是该步骤中通过该层的输入数量。
因此,Muon 的 FLOP 开销最多为 Tm/B,其中 m 为模型维度,B 为以 token 为单位的批量大小,T 为 NS 迭代步数(通常 T=5)。
下面针对两个具体的训练场景计算了此开销:NanoGPT 速通和 Llama 405B 训练。
- 对于当前的 NanoGPT 速通记录,模型维度为 m=768,每批次的 token 数量为 B=524288。因此,开销为 5∗768/524288=0.7%。
- 对于 Llama 405B 训练,模型维度为 m=16384,每批次的 token 数量为 B=16000000(Dubey et al. 2024)。因此,使用 Muon 进行此训练的开销为 5∗16384/16000000=0.5%。
由此可以得出结论,对于典型的语言模型训练场景,无论规模大小,Muon 的 FLOP 开销均低于 1%。
与先前优化器的关系
Shampoo 优化器定义如下:

如果去除预调节器累积,则公式变为以下形式:
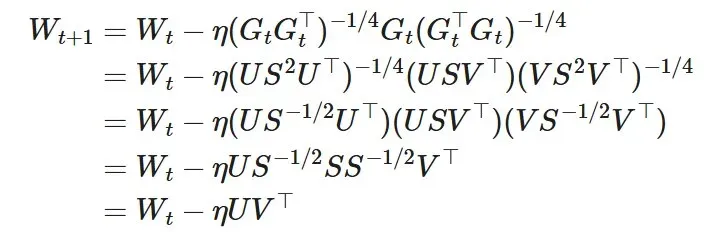
这就是正交化梯度。如果我们在正交化之前添加动量,就能恢复 Muon 更新,但由于使用了四次方根求逆而不是牛顿 - 舒尔茨迭代,因此时间和 FLOP 开销会更高。
因此,可以将关闭动量的 Muon 解读为一种瞬时或无累积的 Shampoo 优化器。
正交 - SGDM
Tuddenham 等人(2022)提出了一种优化神经网络的方法:通过奇异值分解(SVD)对梯度进行正交化,对其结果应用动量,再将动量项作为更新。他们将该优化器命名为正交 - SGDM(Orthogonal-SGDM)。这与 Muon 类似,但区别在于:
- Muon 将动量计算置于正交化之前(实验表明该设计表现更优);
- Muon 采用牛顿 - 舒尔茨迭代代替 SVD,以实现更高效的正交化。
遗憾的是,Tuddenham 等人(2022)在其最佳实验配置(表 3)中报告,他们的方法表现不及精心调参的标准 SGD-Momentum。
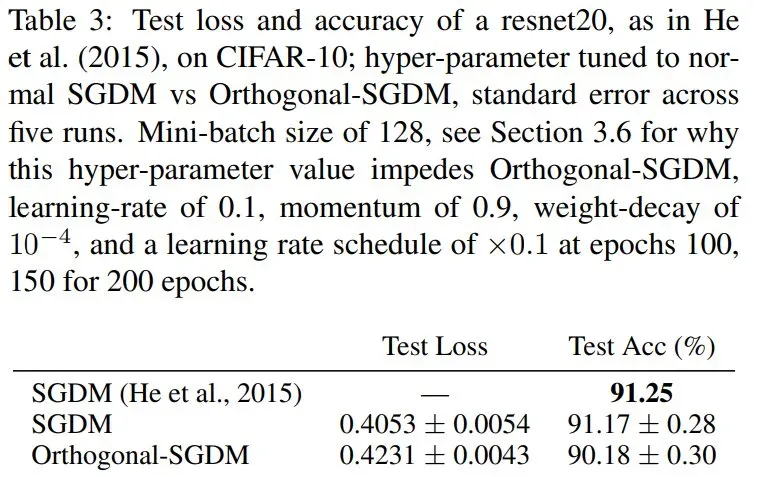
图源:https://arxiv.org/pdf/2202.07052
实验考量
根据设计,Muon 仅适用于 2D 参数(对于卷积滤波器则需展平处理),因此网络中的其余标量和向量参数仍需使用标准优化方法(如 AdamW)。实验发现,输入层和输出层参数即使属于 2D 结构,也需使用 AdamW 优化,这对性能至关重要。具体而言,在训练 Transformer 模型时,词嵌入层(embedding)和最终的分类器头(classifier head)应使用 AdamW 才能达到最佳效果。
嵌入层的优化动态应与其他层不同,这一结论符合模范数理论(modular norm theory)的预测;但输出层的优化动态差异并未被该理论涵盖,而是由实验观测结果驱动。
另一个纯粹的经验结果是,在本文测试的所有案例中,使用 Nesterov 式动量对 Muon 的效果都比普通的 SGD 动量略好。因此,本文在公开的 Muon 实现中将其设为默认设置。
第三个结果是,如果将 Muon 分别应用于 Transformer 的 Q、K、V 参数,而不是同时应用于 Q、K、V 参数,则 Muon 在优化 Transformer 方面效果更佳,因为 Transformer 实现会将 Q、K、V 参数设置为单个线性层,并将输出拆分。
讨论
当前的神经网络优化研究文献中,充斥着大量宣称「大幅超越 AdamW」却最终被社区弃用的优化器。坦白说,这种现象并不令人意外。考虑到行业每年投入数十亿美元用于神经网络训练(且迫切希望降低成本),如果这些优化器真的有效,理应被广泛采用。因此,问题显然出在研究层面而非应用层面 —— 即现有研究存在系统性缺陷。
通过仔细分析相关论文可以发现,最常见的症结在于基线模型(baseline)调优不足:许多研究在将新提出的优化器与 AdamW 对比时,未能对 AdamW 基线进行充分调参。
发表声称有巨大改进但无法复制 / 达到宣传效果的新方法并非无害犯罪,因为它浪费了大量个体研究人员和小型实验室的时间、金钱和士气,他们每天都在为复制和改进这些方法的失败而感到失望。
为了纠正这种情况,我们应该采用以下标准:研究社区应该要求,新的神经网络训练方法应该在竞争性训练任务中表现出色。
竞争性任务通过两种方式解决基线调优不足的问题。
首先,竞争性任务中的基线是先前的最佳记录,如果该任务很热门,这个基线很可能已经被充分调优。
其次,即使在不太可能的情况下先前记录未被充分调优,系统也可以通过恢复到标准训练方法的新记录实现自我修正。这种自我修正之所以可行,是因为标准方法通常具有经过硬件优化的高效实现,而新方法通常会引入额外的计算时间开销。这样一来,在热门的竞争性任务中,标准方法出现重大但虚假的改进并长期保持在记录历史中的可能性就很小了。
这篇博客还列举了一些待解决问题:
- Muon 能否扩展到更大规模的训练?
- Muon 使用的 Newton-Schulz 迭代能否在大规模 GPU 集群中合理分布?
- Muon 是否可能仅适用于预训练,而无法用于微调或强化学习工作负载?
在撰写本文时,Keller Jordan 还不知道这些问题的答案。
不过,已经有研究基于 Muon 优化器进行了改进,比如月之暗面在 Muon 中引入了标准的 AdamW(Loshchilov 等人,2019)权重衰减机制。结果表明,带权重衰减的 Muon 优于原始 Muon 和 AdamW,获得了更低的验证损失。
另外,虽然 Muon 诞生于一篇博客,但也已经有研究团队 Essential AI 发布了对该优化器的系统性研究论文。感兴趣的读者可扩展阅读:

- 论文标题:Practical Efficiency of Muon for Pretraining
- 论文地址:https://arxiv.org/pdf/2505.02222
该论文表明,在计算 - 时间权衡方面,Muon 比 AdamW 更能显著扩展帕累托边界。他们发现,Muon 在保持大批量(远超所谓的临界批量)数据效率的同时,计算效率也更高,从而能够实现更经济的训练。
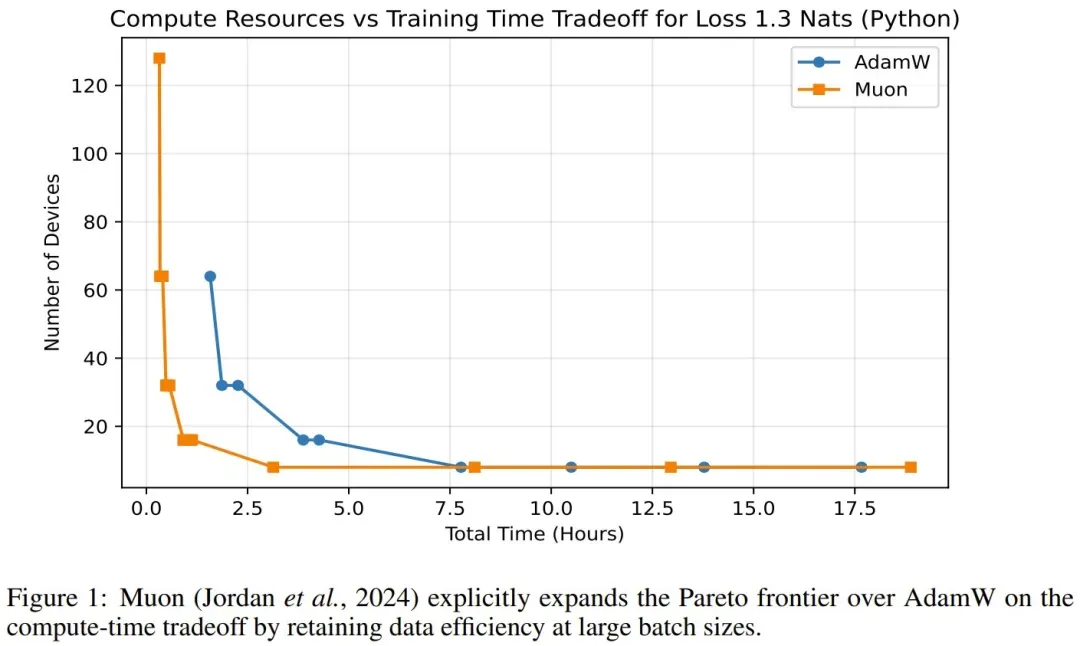
你尝试过 Muon 吗?



