在过去几年里，大语言模型（LLM）与深度学习的浪潮席卷了几乎所有计算领域。从医学诊断到金融建模，从化学分子设计到物理模拟，这些模型在推理任务上的表现一次次刷新了人们的认知。
它们不仅能处理复杂的自然语言，还能跨越模态边界，将图像、语音、代码等信息融会贯通，展现出惊人的“多才多艺”。
然而在这股热潮背后，一个更为基础的问题却始终悬而未决——我们究竟能否量化并刻画人工智能推理能力的极限？
当前的理论体系对这一问题的回答并不充分。虽然我们知道神经网络在足够的训练和数据条件下具有极强的表达能力，但这种“能力”究竟能延伸到哪些推理类型、能否覆盖所有可计算的算法、在复杂度上又有何代价，这些问题依然缺乏系统的数学刻画。
换句话说，我们对“AI推理的边界”缺乏一个可验证、可量化的理论框架。
近日，arXiv 热文《Quantifying The Limits of AI Reasoning:Systematic Neural Network Representations of Algorithms》直面了一个核心问题：在理想化的训练条件下（无限完美数据与完美优化），神经网络究竟能执行哪些类型的推理任务？
现有的通用逼近定理虽然证明了神经网络可以逼近任意连续函数，但它们往往将函数视为“黑箱”映射，忽略了函数背后的算法结构与推理链条。这种忽视意味着，我们无法从逼近理论中直接推导出网络在执行具体推理任务时的复杂度与可行性。
研究目标是通过引入电路复杂度的视角，将推理任务视为电路计算过程，并建立一种系统化的方法，将任意电路精确映射为ReLU前馈神经网络。
这不仅能量化网络的推理能力，还能揭示网络规模与算法运行时间之间的关系，从而为“AI推理极限”提供一个可计算的度量标准。
研究团队来自加拿大麦克马斯特大学数学与统计系，并与向量人工智能研究院（Vector Institute）紧密合作。团队成员在数学逻辑、计算复杂度、神经网络理论等领域都有深厚积累，既具备严谨的理论功底，又熟悉AI前沿应用的需求。
这种跨学科背景，使他们能够在抽象的数学框架与具体的AI推理任务之间架起桥梁。
1.相关研究与理论基础
要理解这项工作的意义，必须先回顾通用逼近定理的历史与局限。上世纪80年代末，Hornik、Cybenko、Funahashi等人的经典结果证明，具有足够隐藏单元的前馈神经网络可以在任意精度下逼近任意连续函数。
这一发现奠定了神经网络表达能力的理论基础，也为深度学习的兴起提供了信心。然而，这类定理关注的是“函数映射”层面的能力——它们并不关心函数是如何被计算出来的，更不涉及计算过程的结构与复杂度。
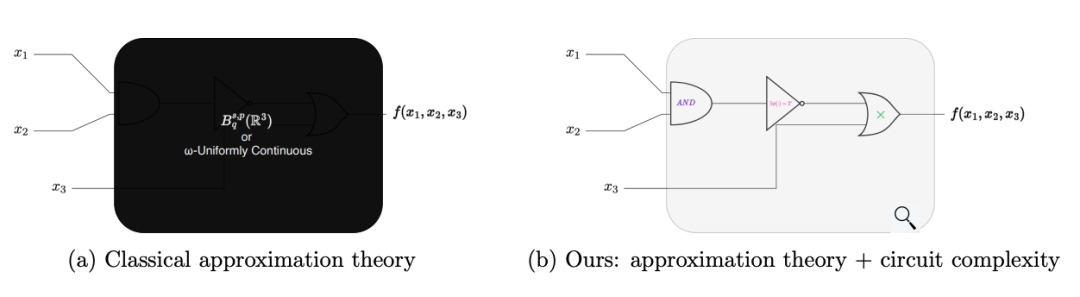图1：比较：经典近似理论与我们的复杂性理论改进。
相比之下，电路复杂度理论则从另一个角度刻画计算能力。它将算法视为由基本运算单元（门）组成的电路，研究在给定门集下实现某个函数所需的最小电路规模与深度。
不同类型的电路——布尔电路（处理逻辑运算）、算术电路（处理加法与乘法）、热带电路（处理最小值与加法）——对应着不同类别的推理任务。
在形式化表示上，这些电路的计算过程可以抽象为有向无环图（DAG）。DAG的节点代表计算步骤，边表示数据流动。输入节点接收原始数据，计算节点执行基本运算，输出节点给出最终结果。
这种结构化表示不仅揭示了算法的执行顺序，也为分析推理链条提供了天然的工具。
有趣的是，这种“推理链”与大语言模型中的Chain-of-Thought（CoT）概念高度契合。
LLM在多步推理时，会生成一系列中间推断步骤，逐步逼近最终答案；而在电路模型中，这些中间步骤正对应着DAG中的计算节点。由此，LLM的推理链可以被视为一种特殊的电路执行过程，这为将AI推理能力映射到电路复杂度框架中提供了理论基础。
图片
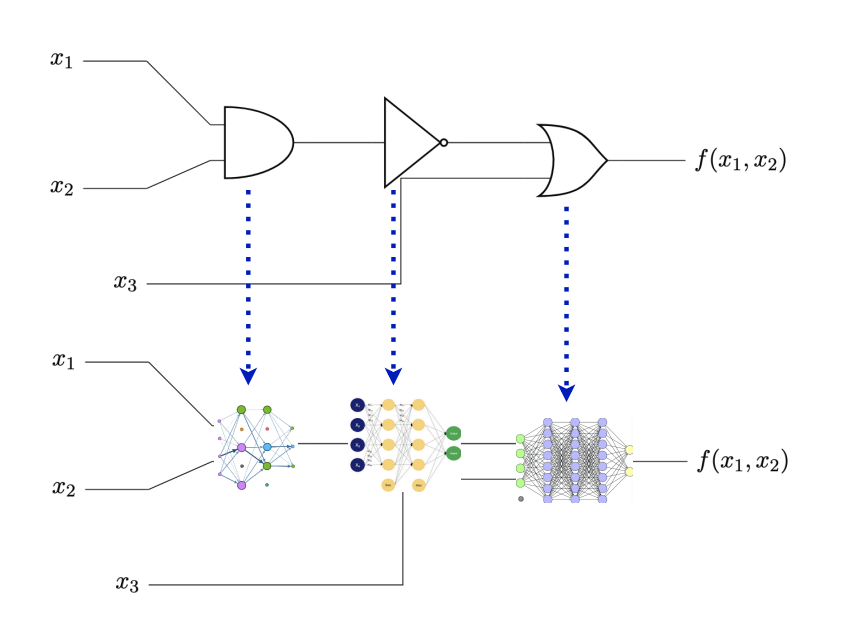
图2：主要结果总结：给定可计算函数作为电路的任何（近似）表示，我们用一个基本的ReLU神经网络（从预先指定的字典中选择）替换每个计算节点，该网络模拟相应的计算。
通过将通用逼近理论与电路复杂度结合，研究团队为我们提供了一个新的视角：不再仅仅问“神经网络能否逼近某个函数”，而是问“神经网络能否高效地模拟计算该函数的算法过程”。这正是量化AI推理极限的关键所在。
2.研究方法与核心构造
这项研究的核心，是一套研究团队称之为“系统化元算法（Meta-Algorithm）”的构造方法。它的野心很大——无论你手里拿的是布尔电路、算术电路、热带电路，还是混合逻辑与算术的复杂计算图，这个方法都能将它一步步“翻译”成一个等价的 ReLU 前馈神经网络，而且是精确模拟，不是近似。
实现的思路很直观，先把算法抽象成一个有向无环图（DAG），每个节点就是一个“门”（gate），执行某种基本运算。然后针对每种门类型，事先准备一个标准化的 ReLU MLP模块作为“模拟器”。
接下来，通过一种被研究团队形象地称为“电路手术（Circuit Surgery）”的操作，把原电路中的节点逐一替换成对应的 MLP 模块，并重新接好输入输出的连线。这样，原电路的计算流程就被无缝嵌入到神经网络的计算图中。
这种“手术”有几个关键要求：替换后的网络必须保持原有的计算依赖关系（Graph Structure Preservation），也就是说，网络的拓扑结构要和原电路的 DAG 一一对应。
同时，网络的规模——也就是神经元和参数的数量——要和原电路的复杂度成比例（Complexity Mapping），实现空间复杂度与时间复杂度的直接映射。
为了让这种映射在真实计算机上成立，研究团队还引入了数字计算模型的细节。现实中的计算不是在连续实数域上进行的，而是在有限精度的数值网格上运算。
技术论文中明确了模运算（modular arithmetic）和舍入机制（rounding scheme）的定义，并提出了“机器精度下的函数等价性”——如果两个函数在给定精度的数值网格上输出完全一致，就认为它们是等价的。这为后续的精确模拟提供了严格的判据。
3.主要理论结果
Theorem 1：通用推理（Universal Reasoning）
这是全文的基石性结论。
它断言任意由特定门集 GG 构成的电路，都可以通过完全无缺陷的“电路手术”转化为一个 ReLU 前馈网络，并且在数字计算机上精确复现原电路的功能。
更重要的是，这个网络的空间复杂度（神经元数量）与原电路的时间复杂度（门数量）同阶，计算图的形状也与原电路一致。这意味着，神经网络不仅能“算对”，还能“按原算法的节奏去算”，真正实现了推理过程的结构化保真。
Theorem 2：有限精度下的通用电路设计
如果说 Theorem 1 解决了“能不能模拟”的问题，Theorem 2 则进一步回答了“有没有遗漏”的疑问。
它证明在有限精度的数值空间上，任何函数都可以由一个 ReLU MLP 精确实现。
这是一个数字计算版本的“超位定理”，与Kolmogorov–Arnold 超位定理在思想上相呼应——后者说任何多元连续函数都可以由单变量函数的叠加表示，这里则说任何有限精度函数都可以由一个通用编码器网络加上线性解码实现。
与经典的通用逼近定理相比，这两个结果的覆盖面更广。通用逼近定理只能保证在无限精度、连续域上的近似，而这里的构造不仅涵盖了逼近，还涵盖了推理任务的精确执行，包括逻辑运算、动态规划、甚至有限步的图灵机模拟。
换句话说，它不仅回答了“神经网络能否学会某个函数”，还回答了“神经网络能否原封不动地执行某个算法”。
图片
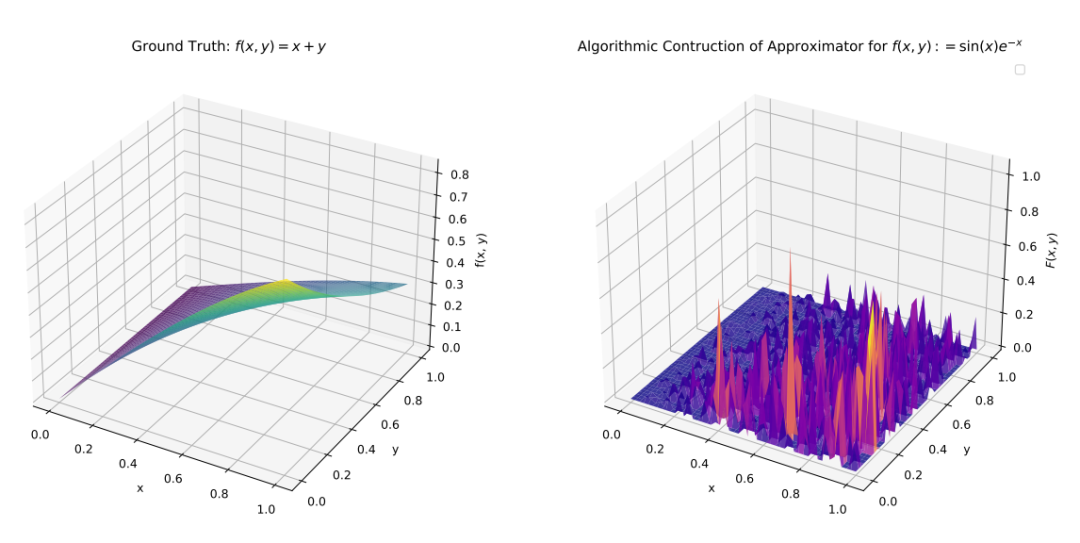
图3：定理2中构造的最坏情况近似值的说明。
这种从电路到网络的系统化映射，让“AI 推理能力”第一次有了可计算、可验证的数学刻画，也为未来在复杂推理任务中设计高效、可解释的神经网络架构提供了坚实的理论支撑。
4.应用案例分析
在理论框架奠定之后，研究团队用一系列推论（Corollary）展示了这一方法在不同类型推理任务中的威力。这些案例不仅是数学上的“存在性证明”，更是对神经网络推理边界的一次次冲击。
布尔函数实现复杂度优化（Corollary 1）
传统上，某些布尔函数的神经网络实现复杂度会呈现双指数级增长，这几乎让直接模拟变得不可行。
研究团队通过系统化元算法，将这种复杂度压缩到单指数级，逼近已知的理论下界。这意味着，在可计算性边界附近，ReLU 网络的表达效率被显著提升，尤其是在需要精确逻辑推理的任务中。
随机化逻辑电路去随机化（Corollary 2）
在经典计算理论中，随机化布尔电路常被用来简化某些问题的实现。但研究团队证明，这些电路可以被等价的确定性 ReLU 网络替代，且不损失功能。
这不仅是一次“去随机化”的胜利，也为构建可验证、可审计的推理网络提供了路径——毕竟，确定性意味着可重复性和可追溯性。
有限时间图灵机模拟（Corollary 3）
更具冲击力的是，研究团队展示了如何用 ReLU 网络精确模拟有限步运行的图灵机，并保留显式的推理链。
这种模拟不是黑箱式的，而是结构上对应原图灵机的状态转移与符号操作，让网络的每一步计算都能被解释为具体的算法步骤。
动态规划与图计算（Corollary 4）
在图计算领域，研究团队以全点对最短路径（All-Pairs Shortest Path, ASP）问题为例，构造了一个立方复杂度的 ReLU 网络实现。
这种实现不仅保留了动态规划的递推结构，还在网络中显式编码了图的拓扑信息，展示了神经网络在结构化推理任务中的潜力。
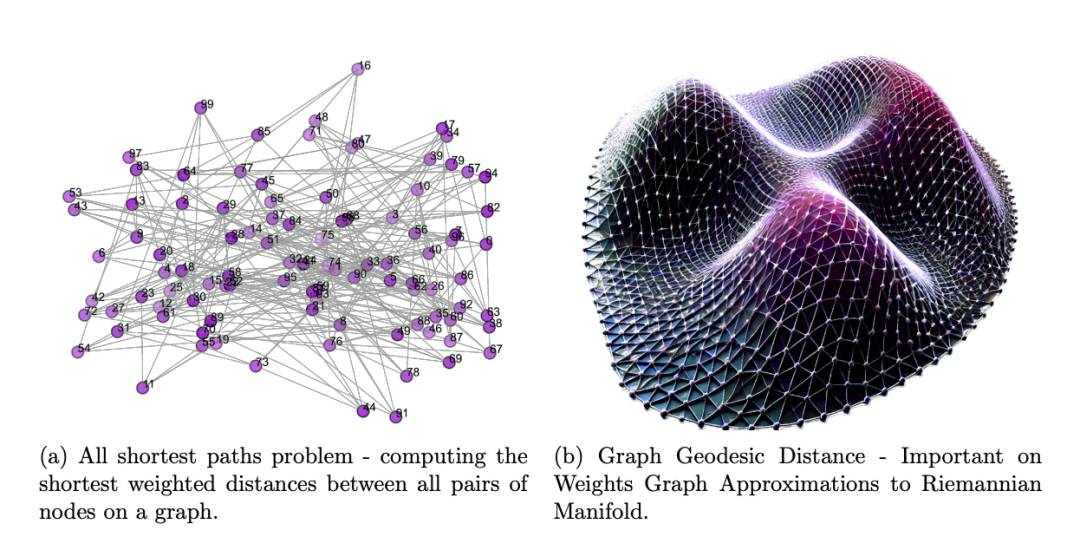图4：几何深度学习中图形的极值示例。
推理能力蕴含通用逼近（Corollary 5）
最后研究团队指出，如果一个网络能够执行上述推理任务，那么它在有限精度下也必然具备通用逼近能力。
换句话说，推理能力本身就涵盖了函数逼近的能力——而且是精确的、非近似的。这为“推理优于逼近”的观点提供了坚实的理论支撑。
5.理论意义与创新点
这项工作的意义，不仅在于提出了一个新的构造方法，更在于它建立了一个统一的理论框架，将电路复杂度、可计算性理论与神经网络的表达能力紧密连接起来。
过去我们常用“通用逼近定理”来描述网络的潜力，但那只是函数映射的视角；现在，我们有了一个能直接刻画算法过程的工具。
这种方法的另一个亮点是推理可解释性。由于网络的计算图与原算法的步骤一一对应，我们可以直接在网络结构中“看到”推理链条。这对于需要审计、验证或调试的高风险应用（如金融合规、医疗诊断）尤为重要。
在复杂度可量化方面，研究团队明确了网络规模与算法复杂度之间的关系，使得我们可以在设计阶段就预测所需的计算资源。这种可预测性为工程实现和硬件部署提供了坚实的基础。
最重要的是，这项研究超越了逼近理论的局限。它不再停留在“网络能否逼近某个函数”的问题上，而是直接回答“网络能否精确执行某个算法”。这为未来构建具备可验证推理能力的神经网络架构打开了新的大门，也为 AI 推理的可计算性研究提供了新的坐标系。
6.未来研究方向
这项研究虽然已经为“神经网络能否精确执行算法”给出了坚实的理论答案，但研究团队也清楚，这只是一个起点。未来的探索空间，既有数学上的深水区，也有工程落地的广阔天地。
首先，是扩展到非欧几里得与无限维输入输出的挑战。当前的构造主要针对欧几里得空间中的有限维向量输入输出，而现实中的许多推理任务——比如图结构分析、流形上的信号处理、甚至函数空间上的算子求解——都天然处于非欧几里得或无限维环境中。
如何在这些空间中定义“电路手术”，并保持计算图的结构保真，将是下一步的关键。这不仅涉及到拓扑与几何的嵌入问题，还可能引入谱图理论、核方法等工具，为神经网络的推理能力开辟新的维度。
其次，是将经典逼近构造（如小波、样条）转化为电路表示。小波分解、B样条插值等方法在信号处理和数值分析中有着成熟的理论与高效的实现，如果能将它们系统化地转化为电路，再映射到 ReLU 网络，就能把这些“人类设计的高效基”直接注入到神经网络的结构中。
这不仅可能带来更紧凑的网络规模，还能在特定任务上获得更强的归纳偏置，让网络在训练样本有限的情况下依然保持高精度推理。
最后是结合几何深度学习与算子学习的应用场景，几何深度学习（Geometric Deep Learning）强调在图、流形、群等结构化空间中进行学习，而算子学习（Operator Learning）则关注从函数到函数的映射，例如求解偏微分方程或模拟物理系统。
将本研究的“算法到网络”映射方法与这两类前沿方向结合，有望构建出既能保留推理链条、又能处理复杂结构化数据的通用推理网络。例如，在分子模拟中，网络可以直接嵌入化学反应的算法流程；在气候建模中，网络可以精确执行数值积分与边界条件处理。
可以预见，这些方向的推进，将让神经网络的推理能力从“能做”走向“能解释、能泛化、能迁移”，并最终在科学计算、工程设计、金融建模等高价值领域释放出更大的潜力。（END）
参考资料：https://arxiv.org/pdf/2508.18526
