卷积神经网络（Convolutional Neural Network，简称CNN）是一种深度学习模型，专门用于处理和分析视觉数据，在图像识别、目标检测等任务中表现尤为出色。
然而，CNN的架构因其固有的复杂性和快速演进的特性，往往难以掌握。
在本文中，将详细介绍标准CNN架构及CNN家族中的各类模型，并拆解其核心组成部分，包括：
- 卷积层、
- 池化层、
- 全连接层
同时讲解步长（stride）、卷积核（kernel）、池化（pooling）等关键概念。
什么是卷积神经网络（CNN）
卷积神经网络（CNN） 是一种特殊类型的神经网络，其设计灵感来源于人类大脑的视觉皮层。
与传统神经网络将图像视为扁平像素数组的处理方式不同，CNN采用分层结构，通过学习从边缘、曲线等简单模式到复杂物体、纹理的特征，逐步构建对视觉数据的理解。
其核心功能是通过多层带神经元的网络结构，自适应地从输入数据中学习空间特征层次。
下图展示了标准CNN架构在图像分类任务中的工作流程：
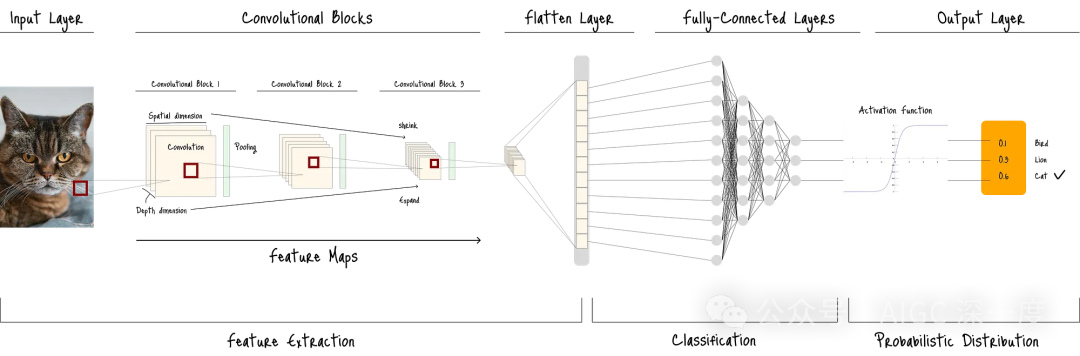图A: 标准CNN架构
CNN的架构由一系列图层组成，每个图层执行特定操作以提取和转换特征。
在下一部分中，将从“卷积块”开始讲解——卷积块是CNN中用于从输入图像中检测独特特征的核心组件。
卷积块
卷积块（Convolutional Block）是CNN的基础构建单元，由一组用于从输入数据中提取特征的图层组成。
如图A所示，这些卷积块相互堆叠，构成CNN架构的核心部分。
下图详细展示了一个标准卷积块的结构，包含1个卷积层（橙色区域）和1个池化层（绿色区域）：
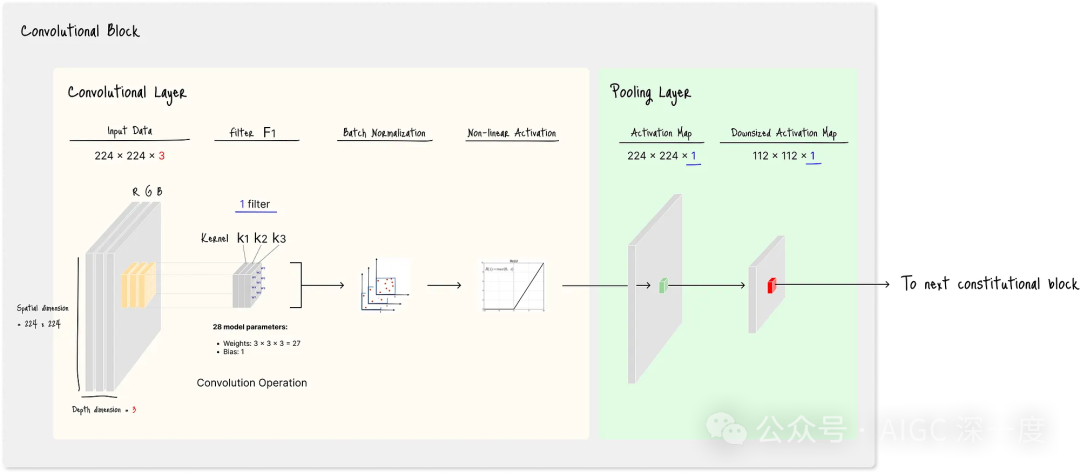图B_含单个滤波器的标准卷积块架构
图B_含单个滤波器的标准卷积块架构
尽管不同CNN架构中卷积块的具体图层可能存在差异，但标准卷积块通常包含：
- 1个或多个卷积层
- 1个池化层
卷积层
卷积层是卷积块的核心，负责检测输入数据中的特定特征。
如图B所示，卷积层的架构包含滤波器（filter） 、批量归一化（batch normalization） 和非线性激活函数（non-linear activation） 三个部分。
其中，滤波器由多个卷积核（kernel，即小型数值矩阵） 组成，通过执行卷积运算（convolutional operation） ，将输入数据中的特定特征突出显示为特征图（feature maps） 。
随后，卷积层对这些特征图应用批量归一化和非线性激活函数，再将处理后的结果传递给池化层。
卷积运算
卷积运算是一个“元素级乘法-求和”过程，帮助网络识别边缘、纹理、形状等特征。
图B中的架构使用了含3个3×3卷积核的单个滤波器——这是因为输入数据具有3个深度维度（深度维度数量与卷积核数量必须保持一致）。
每个3×3卷积核包含9个权重矩阵作为其参数，因此：
- 单个卷积核的参数数量：9个权重
- 单个滤波器的参数数量：3个卷积核 × 9个权重 = 27个权重 + 1个偏置项（bias term）= 共28个可学习模型参数
这些模型参数会在训练过程中不断优化。
滤波器
滤波器由卷积核组成，滤波器的数量直接影响输出特征图的深度。
例如，2个不同的滤波器会生成2个不同的特征图，最终形成深度为2的输出：
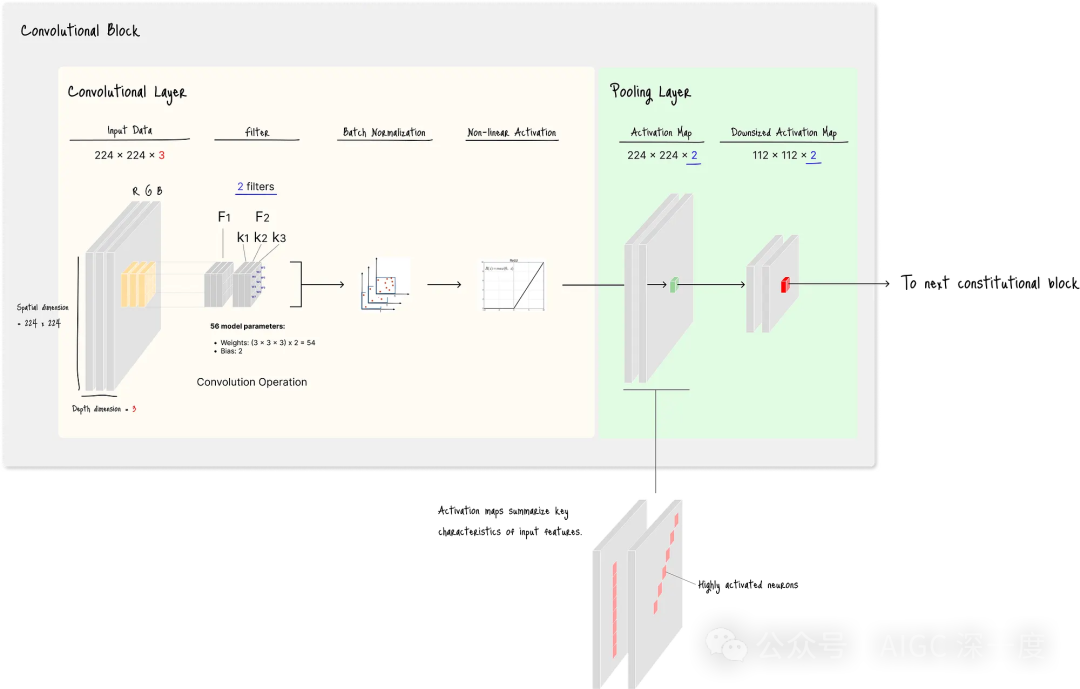图C. 含两个滤波器的标准卷积块架构
图C. 含两个滤波器的标准卷积块架构
在图C中，由于卷积层使用了2个滤波器，生成了2个特征图，因此池化层最终输出2个激活图（activation maps） 。
每个激活图中都包含高度激活的神经元（图C中的粉色单元格），激活程度取决于该激活图所捕捉的特征类型。
由此可见，使用更多滤波器能让网络从输入数据中捕捉更多样化的特征，这对于识别现实世界物体等变异性较高的任务尤为适用。
但另一方面，增加滤波器数量会显著增加可学习模型参数的数量：
- 图B（1个滤波器） ：每个卷积层含28个参数
- 图C（2个滤波器） ：每个卷积层含56个参数
参数增加会导致：
- 训练时间延长
- 内存占用增加
- 过拟合（overfitting）风险上升
因此，在CNN架构设计中，找到“滤波器数量”与“模型性能/效率”的平衡是关键。
卷积运算的数学表达式
卷积运算的过程是：卷积核在输入数据上滑动（或“卷积”），将卷积核中的数值与当前覆盖的图像块（image patch）的对应像素值相乘，再将所有乘积结果求和，最终得到特征图中的单个数值。
若将输入数据表示为I，卷积核表示为K（其中M为卷积核的高度维度，N为宽度维度，例如图B中M=N=3），当前像素坐标表示为(i, j)，则该过程的数学表达式为：
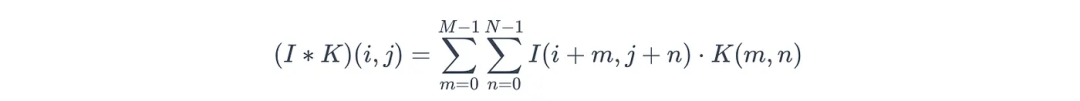图片
其中：
- (I ∗ K)：特征图（输入图像I与卷积核K通过互相关运算（cross-correlation） 得到的卷积结果）
- (i, j)：当前像素的坐标
- I：输入数据（矩阵），I(i, j)表示第i行、第j列像素的数值
- K：卷积核矩阵（维度为M×N）
- K(m, n)：卷积核第m行、第n列的权重值（对应图B中的w₁至w₉）
例如，下图展示了使用索贝尔卷积核（sobel kernel） （一种二维卷积核）执行的卷积运算：
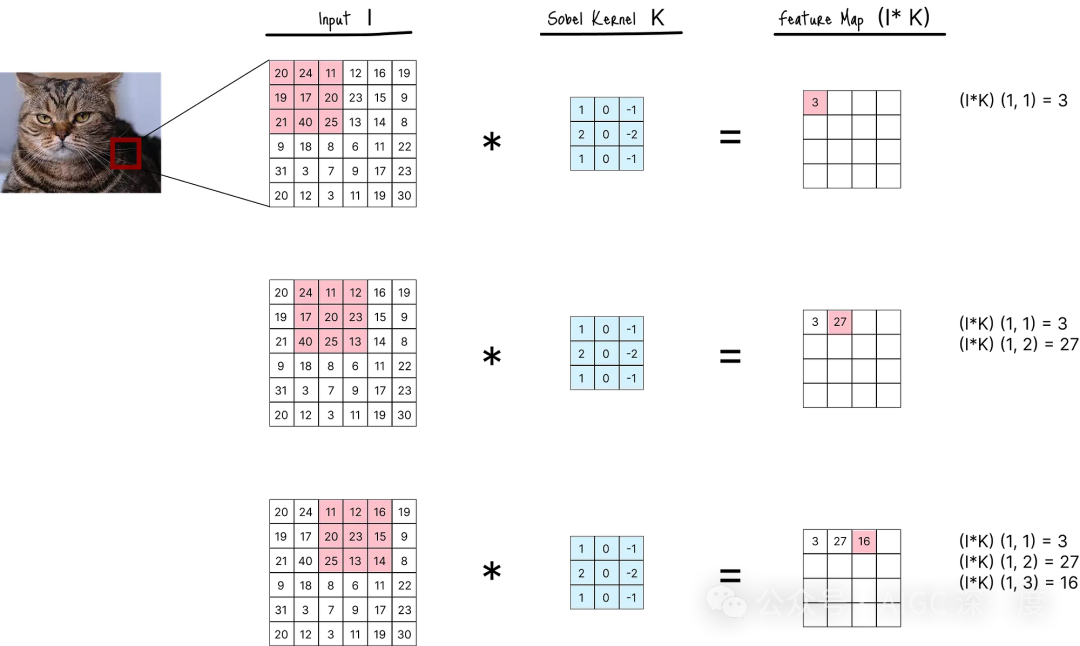图D 索贝尔卷积核的卷积运算过程
在图D中，卷积运算首先对初始的3组坐标(i, j)= (1, 1)至(i, j) = (1, 3)执行计算。
在实际应用中，该过程会对输入I中所有可能的坐标组重复执行，最终生成完整的特征图。
步长（stride） 和填充（padding） 是决定卷积核需处理多少组坐标的关键参数。
步长与填充
步长（stride） 指卷积核在输入矩阵上滑动时每次移动的像素数。
在图D中，步长设置为1，即卷积核每次计算后向右移动1个像素。
尽管步长为2或更大的情况并不常见，但步长越大，最终输出特征图的尺寸越小。
填充（padding） 是在输入图像边缘添加额外像素的技术，主要用于：
- 保留空间维度：卷积运算会缩小输出特征图的尺寸，通过在输入图像边缘添加像素，可使输出尺寸等于或大于输入尺寸。
- 避免边缘信息丢失：图像边缘的像素仅被卷积核处理少数几次，而中心像素会被多次处理。填充能确保所有像素被平等处理，避免重要边缘信息的丢失。
默认的填充设置是有效填充（valid padding，也称“无填充”） ：不在输入图像边缘添加任何像素，卷积核仅在输入图像的有效区域内滑动，最终输出尺寸小于输入尺寸。
与之相对，零填充（zero padding） 是一种常用的填充方式，即在图像边缘添加数值为0的像素。
零填充的常见策略包括：
- Same填充（Same Padding）：添加恰好足够的零像素，使输出特征图的尺寸与输入完全相同。填充量会根据卷积核尺寸和步长自动计算。
- Full填充（Full Padding）：在图像边缘添加大量零像素，确保输入图像的每个像素（包括角落像素）都能成为卷积核的中心。这种方式会使输出尺寸大于输入尺寸。
在图D中，为简化演示，采用了有效填充（无填充）。
若应用零填充，输入数据将呈现为图D’ 的形式，卷积核会在这些填充区域上滑动以执行卷积运算：
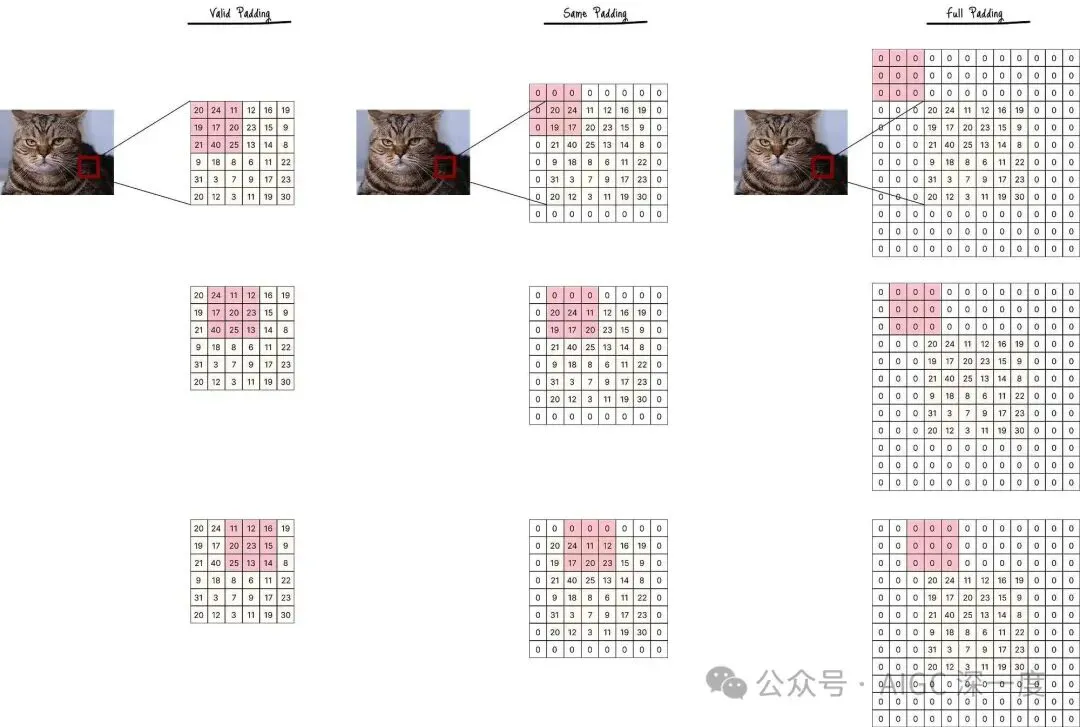图D ：含零填充的输入数据
最后，二维卷积核生成的输出尺寸O可通过以下公式计算：
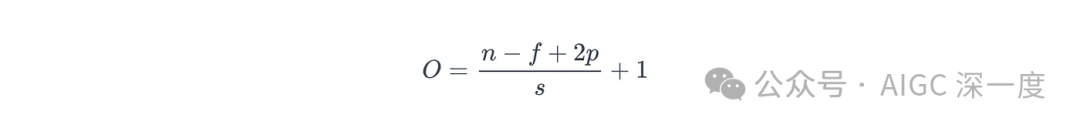图片
其中：
- O：输出特征图的尺寸（高度或宽度）
- n：输入数据的尺寸（高度或宽度）
- f：卷积核的尺寸
- p：填充量（边缘添加的像素数）
- s：步长
以图D’ 为例，已知参数如下：
- n = 6（输入尺寸）
- f = 3（卷积核尺寸）
- p = 0（有效填充）或p = 1（Same填充）
- s = 1（步长）
则不同填充策略下的输出尺寸计算如下：
- 有效填充（p=0）：O = ((6 - 3 + 0) / 1) + 1 = 4 → 小于输入尺寸n=6
- Same填充（p=1）：O = ((6 - 3 + 2) / 1) + 1 = 6 → 等于输入尺寸n=6
- Full填充（p=3，此处需调整p以满足Full填充逻辑）：O = ((6 - 3 + 6) / 1) + 1 = 9 → 大于输入尺寸n=6
这些计算结果清晰展示了填充对输出尺寸的影响。
批量归一化
部分卷积块会在激活函数之前加入批量归一化（Batch Normalization，简称BN）过程。
该过程对特征图进行归一化处理，通过减少内部协变量偏移（internal covariate shift） ，帮助稳定训练过程。
内部协变量偏移是指：在神经网络训练过程中，各层输入数据的分布会发生变化。这种偏移会迫使每一层在每个训练周期（epoch）都重新适应变化的输入分布，从而减缓训练速度。
批量归一化是解决这一问题的常用方案：通过将特征图的均值调整为0、方差调整为1，使输入分布更密集、更稳定，进而加速训练。
非线性激活函数
在卷积层运算的最后一步，会对每个特征图应用非线性激活函数（non-linear activation function） 。
常用的激活函数是ReLU函数（Rectified Linear Unit），其作用是返回输入值（神经元的加权和与偏置之和，记为x）与0中的较大值，公式如下：
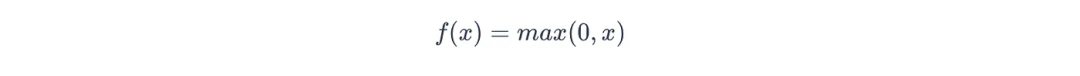图片
该过程为网络引入了非线性特性，使其能够学习复杂的特征模式。
池化层
池化层（Pooling Layer） 通过缩小特征图的空间维度，对特征图进行下采样（downsample），最终生成激活图。
池化层的主要作用包括：
- 降低计算负荷：缩小特征图尺寸，减少后续图层的参数数量和计算量。
- 实现平移不变性（translation invariance）：使网络对输入特征的位置偏移更具鲁棒性，确保即使特征位置发生微小变化，网络仍能识别该特征。
池化层生成的每个激活图，都是对卷积层处理后输入数据特征的“总结”。
池化运算的类型
下图展示了多种常见的池化运算方式：
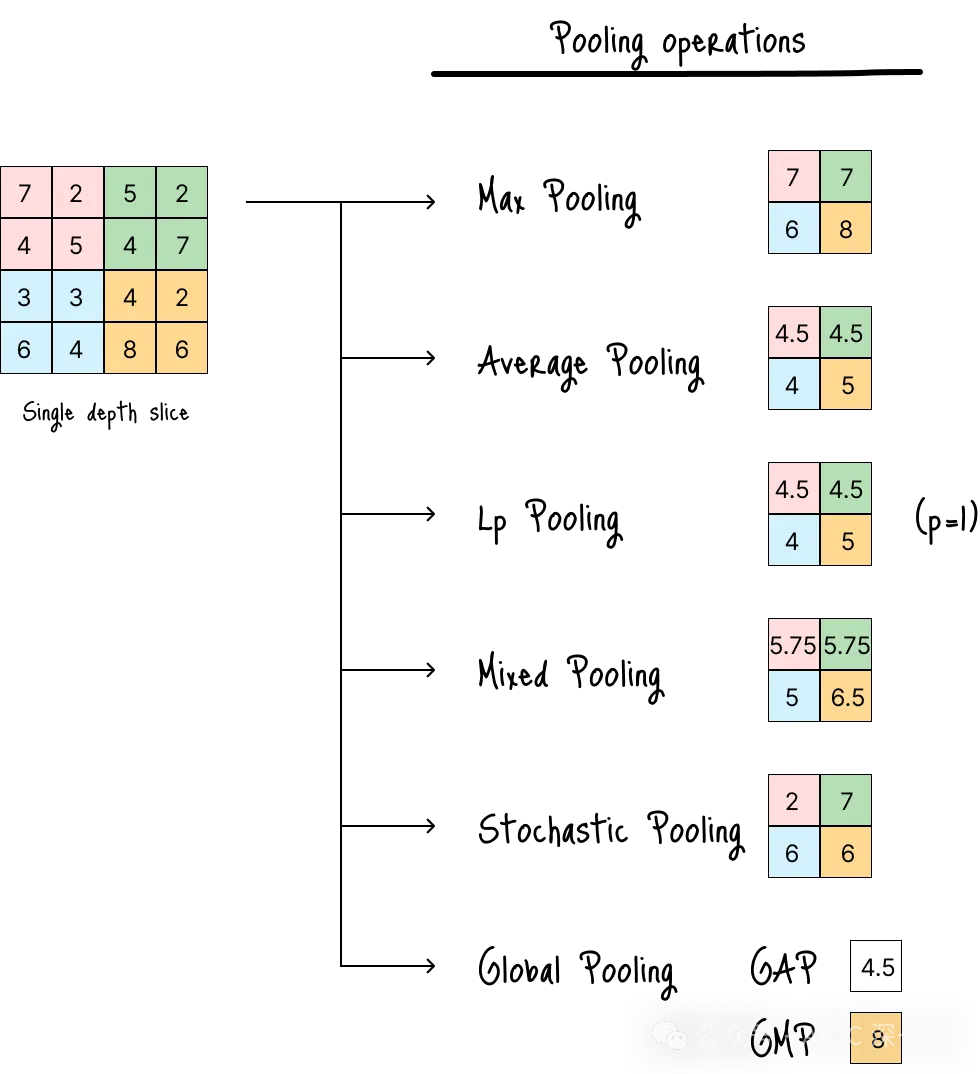步长时的多种池化运算
最大池化（Max Pooling）
最常用的池化方式，从指定区域中选择激活程度最高的特征。
这种方式会提取区域内最显著的特征，同时丢弃其他被认为不重要的特征。
常见应用场景：
- 大多数图像分类任务（目标是识别特征是否存在，而非精确位置）。
平均池化（Average Pooling）
计算池化窗口内所有元素的平均值。
与最大池化不同，平均池化会考虑区域内的所有数值，有助于平滑特征图、减少噪声干扰。
常见应用场景：
- 医学影像分析
- 卫星影像处理
- 任何需要关注区域内特征整体分布（而非单一强信号）的任务。
Lp池化（Lp-Pooling）
一种广义的池化方式，通过计算池化窗口内数值的Lp范数（Lp norm） 实现下采样，最大池化和平均池化均为其特殊情况：
- 当p = 1时，Lp池化等价于平均池化。
- 当p = ∞时，Lp池化等价于最大池化。
常见应用场景：
- 科研领域中的广义池化方案。
混合池化（Mixed Pooling）
对最大池化和平均池化的线性组合。
网络可根据具体任务学习最优的组合比例，灵活性更高。
常见应用场景：
- 科研领域中的广义池化方案。
随机池化（Stochastic Pooling）
与确定性选择（如最大池化选最大值、平均池化算平均值）不同，随机池化会根据数值大小按比例随机采样池化窗口内的激活值。
这种随机性可作为一种正则化手段，帮助减少过拟合。
常见应用场景：
- 处理小型数据集时，用于缓解过拟合的正则化方法。
全局池化（Global Pooling）
与滑动小窗口的池化方式不同，全局池化将整个特征图总结为单个数值。
全局池化通常应用于CNN的卷积部分末尾、全连接层之前，主要有两种类型：
- 全局平均池化（Global Average Pooling，GAP）：计算整个特征图所有元素的平均值。
- 全局最大池化（Global Max Pooling，GMP）：取整个特征图的最大值。
尽管池化方式多样，但所有池化运算的核心目标一致：通过下采样缩小特征图尺寸，降低计算负荷，同时实现平移不变性。
池化层的替代方案
池化层可完全由“大踏步卷积层（convolutional layers with larger stride）”替代。
例如，步长设为2的卷积层可将特征图的空间维度缩小一半，实现与池化层相同的下采样效果。
这种替代方案具有两个显著优势：
- 下采样过程的最优学习：允许网络学习最优的下采样操作，可能构建更具表达能力的模型，提升性能。
- 全程保留空间信息：大踏步卷积不会丢弃区域内的数值，能保留更多输入数据信息，帮助网络捕捉更丰富的上下文。
尤其当所有池化层都被大踏步卷积层替代时，会形成全卷积网络（Fully Convolutional Network，FCN） ——这类网络能在整个训练和推理过程中保留空间信息。
研究表明，全卷积网络更适合需要复杂上下文理解的任务，例如：
- 语义分割（semantic segmentation）
- 异常检测（anomaly detection）
- 目标检测（object detection）
- 图像超分辨率（image super-resolution）
但正如图B和图C所示，增加卷积层会导致可学习参数数量增加，使模型更复杂、计算成本更高。因此，在选择方案时需权衡利弊。
全连接层（FC Layer）
全连接层（Fully Connected Layer，简称FC层） ，又称密集层（Dense Layer） ，是CNN中最后的特征转换部分——该层中每个神经元都与前一层的所有神经元相连。
全连接层的核心作用是：基于卷积块提取的特征图（即特征），做出最终决策。
卷积块提取的特征包括边缘、角落、纹理等局部特征，而全连接层会将这些高层抽象特征整合，用于执行最终任务，例如：
- 分类任务：在图像分类问题中，全连接层会将扁平化后的特征图转换为每个类别的概率。
- 回归任务：在回归问题中，全连接层会输出单个连续值。
扁平化步骤
如图A所示，在全连接层处理特征图之前，需先将特征图转换为单个长一维向量（1D vector）——这一过程称为扁平化（flattening） 。
该步骤是必要的，因为全连接层仅接受一维向量作为输入。
扁平化后的向量将作为第一层全连接层的输入，随后依次传递给后续全连接层进行处理。
注意事项
全连接层擅长学习特征间的全局模式和关联，因此在最终决策步骤中表现出色。
但全连接层的参数数量极大：由于每个神经元都与前一层所有神经元相连，权重数量会迅速增加。
这会导致两个问题：
- 模型过拟合风险上升
- 计算成本增加
为缓解这些问题，通常会采用 dropout 等正则化技术。
输出层
CNN中的输出层（Output Layer） 是生成网络最终输出的关键层。
输出层会接收卷积块和全连接层传递的高层抽象特征，并将其转换为最终的输出形式。
如图A所示，在分类任务中，输出层会对输入应用softmax激活函数，生成预设类别的概率分布（例如鸟类、狮子、猫）。
Softmax函数能确保所有类别的输出概率之和为1，使结果可直接解释为类别概率。
在回归任务中，输出层通常包含1个或多个神经元，采用线性激活函数（或无激活函数），输出连续值。
以上就是CNN架构的完整介绍。
当卷积层提取完特征层次后，CNN的架构会过渡到与标准前馈网络（feedforward network）类似的结构。
在训练过程中，全连接层和卷积核的权重、偏置等可学习模型参数，会通过反向传播（backpropagation）算法不断优化。
卷积神经网络的类型
为应对不同任务挑战，研究者开发了多种CNN架构。
首先，根据卷积核的维度，CNN可分为三类：
- 一维CNN（1D CNNs）
- 二维CNN（2D CNNs，最常见的CNN类型，如图C中使用的索贝尔卷积核）
- 三维CNN（3D CNNs）
下面将分别介绍这三类CNN。
一维CNN（1D CNNs）
一维CNN适用于序列数据（如时间序列分析、自然语言处理），其滤波器仅沿序列的一个维度滑动。
常见应用场景：
- 文本、音频、传感器数据等序列数据的分析与特征提取。
缺点：
- 不适用于需要从图像或视频中提取空间特征的任务——因为一维CNN仅考虑输入数据的一个维度。
二维CNN（2D CNNs）
二维CNN是处理图像和视频数据的标准类型。
如前所述，其滤波器在二维平面上滑动，捕捉空间特征，因此能高效学习空间特征层次。
常见应用场景：
- 图像分类、目标检测等涉及静态视觉数据的任务。
缺点：
- 不适用于体积数据（volumetric data）或具有强时间相关性的序列数据。
主要的二维CNN模型
以下是几种典型的二维CNN架构模型：
LeNet-5
- 手写数字识别领域的开创性模型。
- 适用场景：作为简单图像分类任务（低分辨率图像）的基础模型。
- 缺点：深度和容量有限，不适用于复杂、高分辨率图像任务。
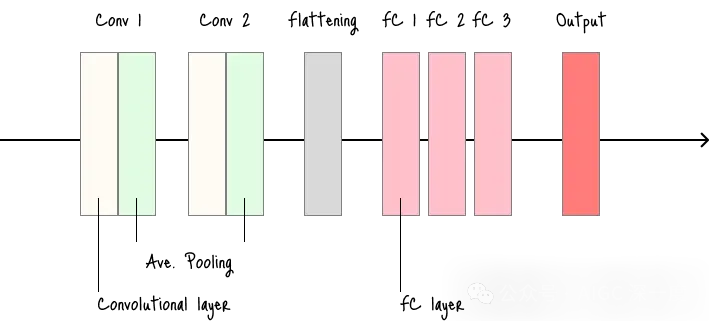LeNet架构
AlexNet
- 比LeNet-5更深、更宽，是推动深度学习普及的关键模型。
- 适用场景：作为比LeNet更强的图像分类基准模型，适用于较大数据集。
- 缺点：以当前标准来看架构较浅；使用的大尺寸卷积核（11×11、5×5）效率较低。
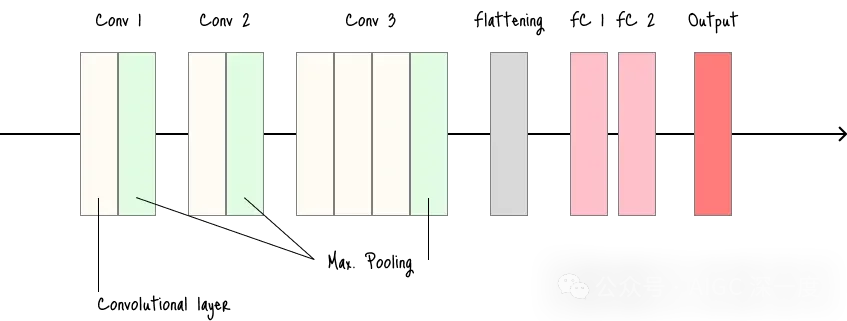AlexNet架构
VGGNet
- 架构简洁统一，通过使用小尺寸（3×3）卷积核增加网络深度。
- 适用场景：作为其他模型的特征提取器（架构鲁棒且易于理解）。
- 缺点：参数数量大、内存消耗高，导致训练和部署速度慢。
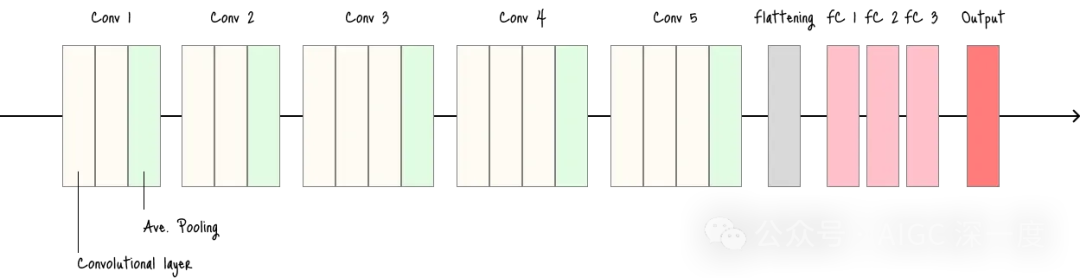VGGNet架构
GoogLeNet
- 深度网络，参数数量较少——核心创新是“ inception模块（inception module）”：该模块允许网络在单个图层内自主选择卷积核尺寸和池化操作。
- 适用场景：需要高性能且计算高效的模型的任务。
- 缺点：架构复杂，理解和实现难度较高。
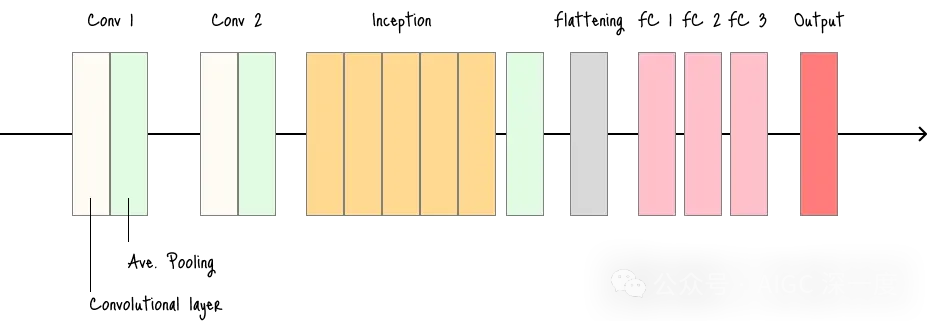GoogLeNet架构
ResNet（残差网络，Residual Network）
- 突破性模型，解决了极深网络中的梯度消失（vanishing gradient）问题。
- 适用场景：任何需要训练极深网络的视觉任务——其残差连接（residual connections）可防止网络深度增加时性能下降。
- 缺点：网络深度仍可能导致训练时间较长（尽管比同等深度的非残差网络更易训练）。
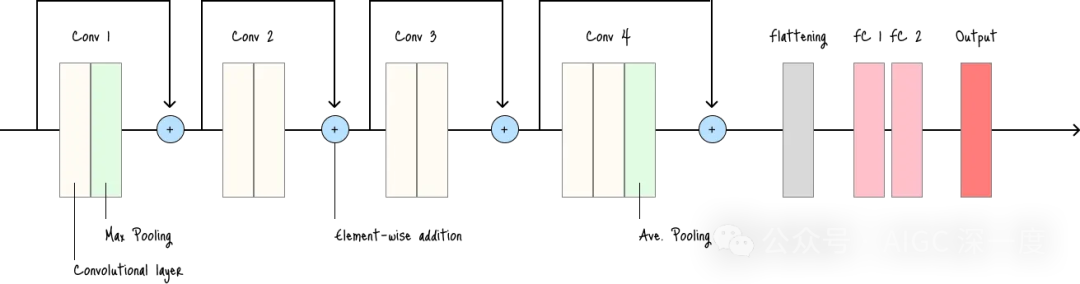ResNet架构
DenseNet（密集连接网络，Densely Connected Network）
- 核心特点是“密集连接”：每个图层都与前向传播路径中的所有其他图层相连。
- 适用场景：内存和计算资源有限的任务。
- 缺点：密集连接会导致特征图数量庞大，内存消耗较高。
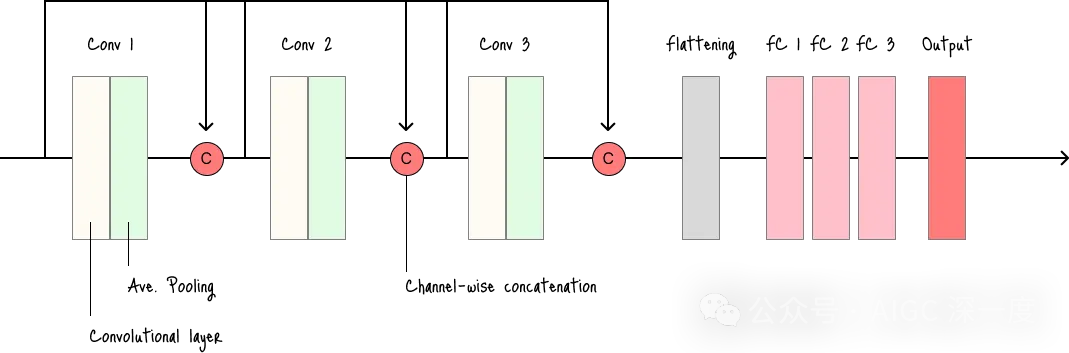DenseNet架构
三维CNN（3D CNNs）
三维CNN适用于体积数据，如医学影像（MRI、CT扫描）或视频分类。
其滤波器在三维空间中运算，可同时捕捉空间和时间信息。
常见应用场景：
- 需同时考虑空间和时间特征进行分类的三维数据任务。
缺点：
- 计算成本高。
- 由于参数数量大，需要大量训练数据。
主要模型：
- DenseNet：尽管DenseNet的常见实现是针对二维卷积，但“密集块（dense blocks）”的核心原理可扩展到三维卷积，适用于医学影像、视频分析等领域。
