大家好，我是肆〇柒。今天要和大家分享的这项突破性研究来自MBZUAI（穆罕默德·本·扎耶德人工智能大学）、莫斯科物理技术学院神经网络与深度学习实验室、莫斯科人工智能研究院以及伦敦数学科学研究所的联合团队。这项研究通过精心设计的1dCA基准，首次清晰地区分了模型的规则抽象能力和多步状态传播能力，为我们理解神经网络的"思考"机制提供了新视角。（本文比较晦涩，慎入。如果你觉得晦涩，依然想继续阅读，可以直接拉到文末看总结）
当大型语言模型在学术竞赛中取得突破性进展时，整个AI界为之震动。像OpenAI的o1和DeepSeek R1模型在2024年美国数学奥林匹克竞赛资格赛（AIME）中获得了前500名的排名，这一成绩足以让它们进入正式的美国数学奥林匹克竞赛（USAMO）。更令人惊叹的是，OpenAI的系统在国际信息学奥林匹克竞赛（IOI 2025）中取得了第6名的优异成绩。与此同时，Google DeepMind和OpenAI的系统在国际数学奥林匹克竞赛（IMO 2025）中均达到了金牌标准，实现了AI在顶级学术竞赛中的里程碑式突破。
然而，在欢呼之余，一个更深层、更本质的问题也随之浮现：这些令人兴奋的表现，究竟是源于模型对海量数据的"记忆"与模式匹配，还是它们确实掌握了人类引以为傲的、循序渐进的"多步推理"能力？
研究表明，当前的LLM，更像是一位擅长"看一步走一步"的棋手，而非能深思熟虑、推演数步的宗师。它的"推理"能力，可能在第一步之后就戛然而止。《Beyond Memorization: Extending Reasoning Depth with Recurrence, Memory and Test-Time Compute Scaling》这篇研究，通过一个精巧的"思想实验"，给出了一个颠覆性的答案：多步状态传播是真正的推理瓶颈，而固定深度是难以逾越的硬约束。这项研究不仅揭示了LLM"思考"的边界，更为我们指明了突破这一边界的具体路径。
一维细胞自动机：神经网络推理能力的"试金石"
要理解这项研究，首先需要了解"一维细胞自动机"(1dCA)这一核心工具。现在想象一排20个灯泡（论文中W=20），每个灯泡只能是亮(1)或灭(0)。这排灯泡就是一维细胞自动机的"状态"。
现在，设定一个简单规则：每个灯泡下一秒的状态，取决于它自己和左右各2个邻居（共5个灯泡）当前的状态。这个规则可以用一个32位的字符串表示（因为5个二进制输入有2⁵=32种可能组合）。
例如，如果规则字符串是"01011111100100000101111011111100"：
- 当5个输入是"00000"时，输出是规则字符串的第0位（即"0"）
- 当5个输入是"00001"时，输出是规则字符串的第1位（即"1"）
- 以此类推...
从一个初始状态（如"10110111001000110100"）开始，反复应用这个规则，就会产生一个随时间演化的状态序列，称为"轨道"(orbit)。
一维细胞自动机示意图：5位窗口决定下一个状态
打造"纯净"的推理试验场——1dCA基准
为什么是细胞自动机？
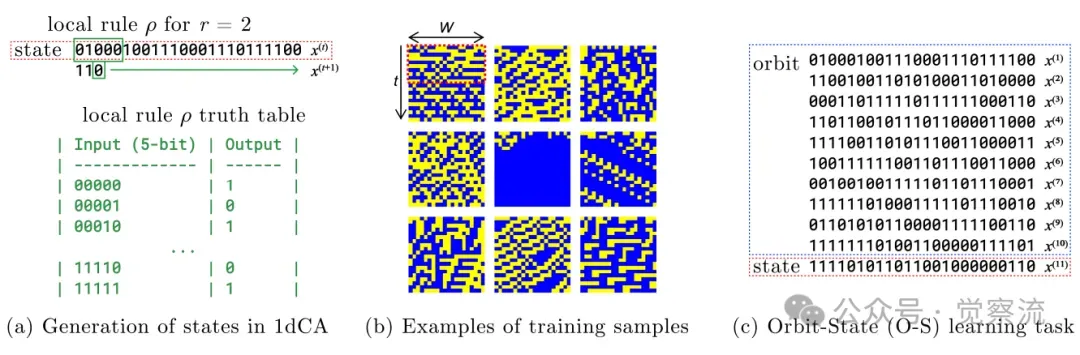
要研究"纯粹"的推理，首先需要一个能完美模拟推理本质的试验场。一维细胞自动机（1dCA）因其简洁而强大的特性，成为了理想之选。在一个1dCA系统中，全局状态由一排二进制细胞构成，其演化完全由一个局部的布尔规则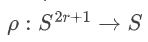 
决定。给定一个初始状态，系统会生成一条确定的演化轨迹（Orbit）。
这个过程天然地映射了人类推理的两个核心阶段：
为什么这个设计很巧妙？ 研究者通过一个关键创新确保了任何观察到的成功都反映了模型对规则的泛化能力，而非简单的数据查找：训练集和测试集所使用的局部规则是完全不重叠的随机集合。这意味着，模型在测试时遇到的每一个规则都是全新的，其成功与否，完全取决于它是否在训练过程中学会了通用的"推理算法"。这种设计将"记忆"的干扰彻底剥离，让我们能清晰地观察到模型真正的推理能力。
一维细胞自动机的学习 (a) 用局部规则更新状态 (b) 1dCA 的“轨道”是一串长度为 W = 20 的二进制字符串序列；最前面 k = 10 个状态（红色框标出）被编码为 Transformer 的输入 (c) 给定轨道的一部分，模型学习预测下一个状态（简称 O-S）
在此基础上，研究者定义了"推理深度"k，即模型需要预测从当前状态起第 k 步之后的状态。为了全面评估模型能力，他们设计了四种任务变体：
这个精心设计的基准，为后续的架构大比拼和策略分析奠定了坚实、可控且无偏的基础，让我们得以在"纯净"的环境中，观察模型推理能力的真相。
基础架构大比拼——效率与深度的残酷现实
在公平的竞技场上，研究者将四种主流架构——Transformer (GPTNeox)、LSTM、状态空间模型 (Mamba) 和关联循环记忆Transformer (ARMT)——置于相同的起跑线：统一使用仅有4层、128维的小型模型。这一设置至关重要，它确保了所有比较都是在固定参数预算下进行的，从而能真实反映出不同架构在效率上的优劣。
实验结果揭示了一个残酷而清晰的现实：单步推理易如反掌，多步推理难如登天。
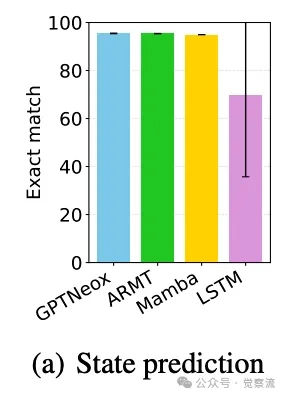
单步准确率近乎完美，但多步性能崩溃
这张图是整个研究的判决书。它宣告了绝大多数神经网络的"死刑"：在单步预测 (k=1) 上，准确率普遍超过95%（LSTM略低，约90%），这证明模型确实学会了从轨迹中抽象出底层规则，完成了第一阶段的推理。然而，一旦任务要求预测两步之后的状态 (k=2)，除了ARMT之外，其他所有模型的准确率都像自由落体一样暴跌至25%以下。这场"断崖式下跌"无情地揭示了一个事实：模型或许"懂"了规则，却完全丧失了应用规则进行连续推演的能力。更令人深思的是O-RS任务的结果。
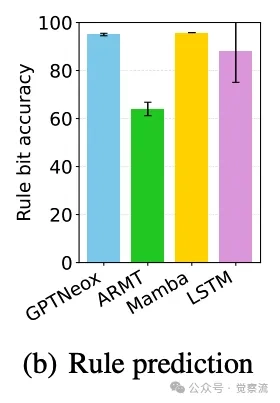
规则预测的高准确率无法转化为多步预测能力
研究者本以为，通过要求模型同时输出规则，直接强化"规则推断"的监督信号，能"手把手"地教会模型如何进行规则推断，从而为多步推理打好基础。但结果却显示，这种直接的监督对提升 k>1 的性能几乎无效。这个"意外"是研究的关键转折点，它将研究者的目光从"规则推断"彻底转向了"状态传播"，揭示出后者才是阻碍模型进行深度推理的真正"拦路虎"。那么，如何突破这个瓶颈？增加模型容量是否有效？研究者通过对比实验给出了明确答案：深度 > 宽度。
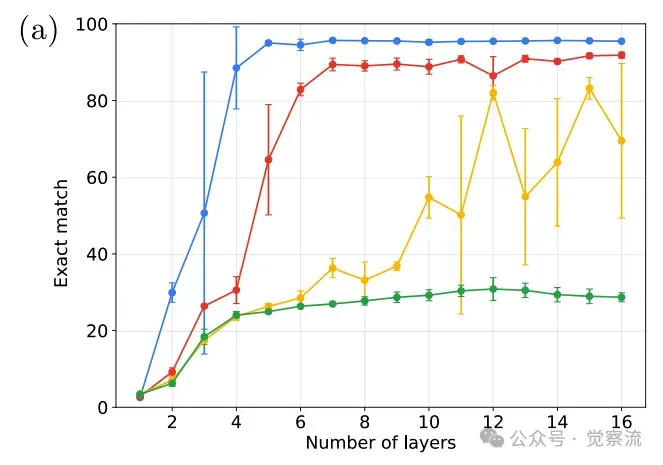
深度扩展显著提升多步预测能力
增加Transformer的层数（纵向深度扩展）能显著提升其在 k=2,3 时的表现。例如，从4层增加到6层，k=2 的准确率从约40%跃升至80%以上；增加到12层，k=3 的准确率也能提升至约60%。相比之下，单纯增加模型的宽度（dmodel）带来的收益则微乎其微。
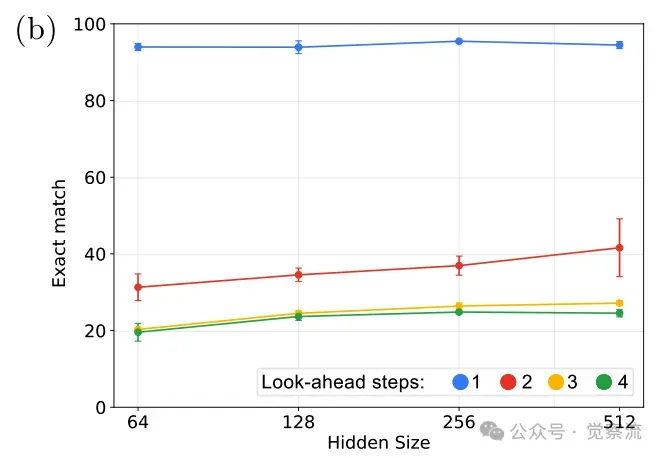
宽度扩展对多步推理收效甚微
当 dmodel 从64增加到128时，性能有小幅提升，但继续增加到256或512，收益几乎可以忽略不计。综上，实验数据清晰地指向一个核心结论：状态传播是比规则推断更深的瓶颈，而突破此瓶颈的根本在于增加模型的纵向深度。
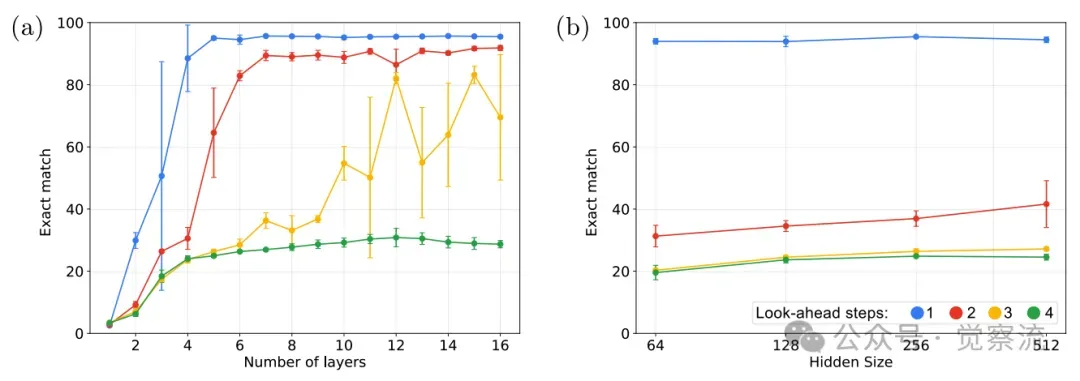
然而上图图（a）也揭示了一个严峻的工程现实：为每个额外的推理步骤都堆叠一层新网络，其成本是线性增长且不可持续的。这自然引出了一个关键的研究命题：我们能否在不增加任何静态参数的前提下，让一个4层的"小"模型，完成6层甚至8层模型才能胜任的多步推理任务？ 带着这个问题，我们继续向后看，探索循环、动态计算与强化学习等"四两拨千斤"的高效策略。
突破瓶颈——如何在不增加参数的前提下扩展"有效推理深度"？
面对固定深度的硬性约束，研究者探索了四种截然不同的策略，每一种都在效率与性能之间做出了独特的权衡。
策略一：引入"循环"架构 (Recurrence) —— ARMT的效率胜利
ARMT（Associative Recurrent Memory Transformer）是这场效率竞赛中的首个赢家。它通过在Transformer架构中引入分段级别的循环和关联记忆，强制模型在处理不同片段时复用和传递信息。具体实现上，输入序列被分割成多个片段（例如，每两个连续状态为一个片段），ARMT在处理完一个片段后，会将其输出的记忆状态传递给下一个片段作为输入。
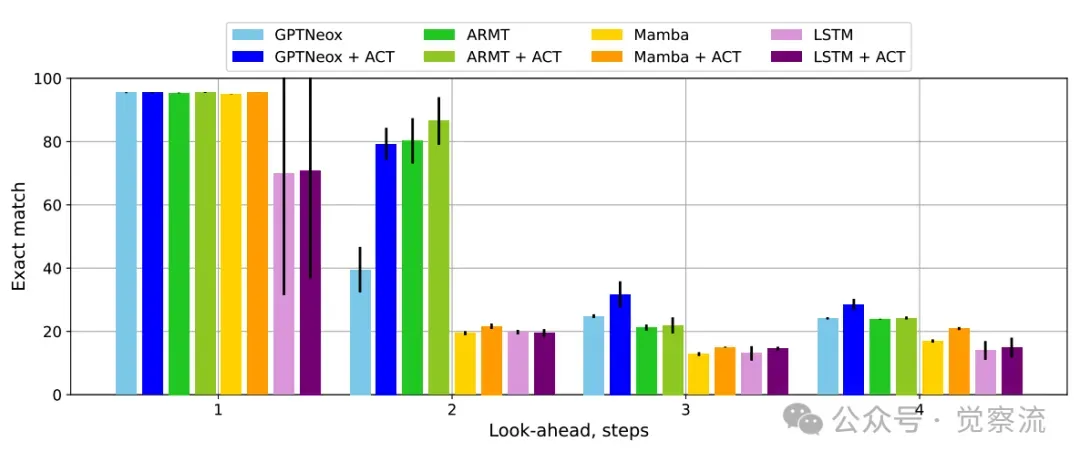
ACT显著提升Transformer类模型的多步预测能力
实验结果显示，ARMT是唯一一个能在4层架构下稳定处理 k=2 任务的基础模型（准确率约43%），而其他4层模型在此任务上的准确率均低于25%。
为什么ARMT能成功？ 关键在于其架构设计强制模型分离规则与状态表示。这种分离使ARMT能够生成一个中间状态的隐藏表示，然后应用规则进行预测，从而在不增加任何静态参数的前提下，动态地扩展了模型的"有效深度"。这是一种典型的参数高效方案，证明了循环机制在克服状态传播瓶颈上的独特优势。然而，其能力也受限于"分段"设计，无法突破 k=2 的上限，表明单纯的架构循环有其固有的边界。
策略二：动态"思考时间" (Adaptive Computation Time - ACT) —— 计算效率的优雅方案
为标准的Transformer（GPTNeox）添加ACT后，其性能在 k=2 时获得了稳定提升（从40%提升至约60%），相当于获得了约"+1步"的有效深度。ACT的精妙之处在于：它通过在测试时动态增加计算量（而非在训练时增加参数量）来换取性能提升，实现了计算高效的深度扩展。进一步的消融实验（FCT vs ACT）
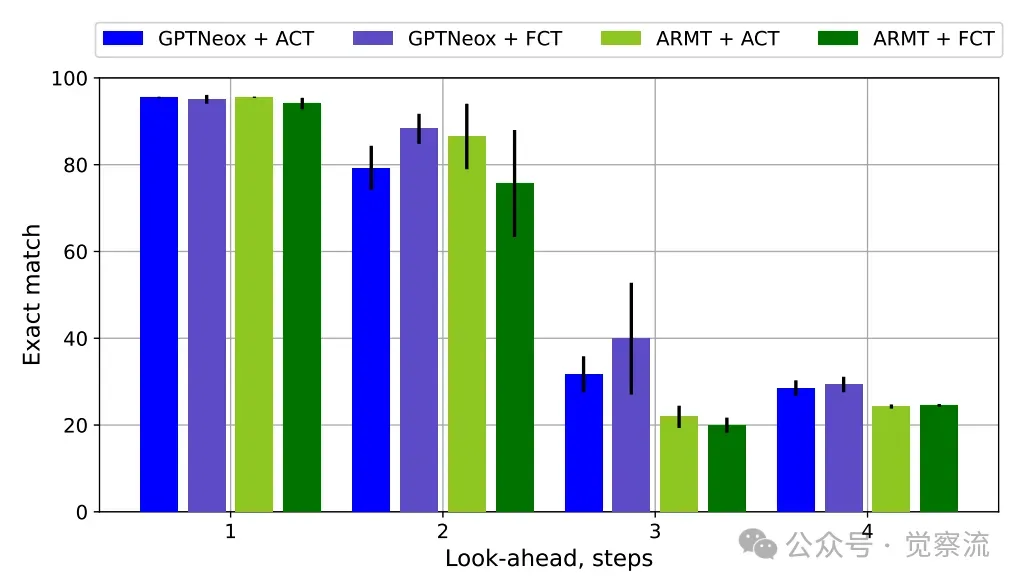
固定计算步数(FCT)与自适应计算时间(ACT)在Orbit-State任务中的比较
揭示了一个关键洞察：ACT的"自适应性"是其价值所在。研究者设置了一个"固定计算步数"（FCT）的基线，强制模型每次都进行3步计算（这是ACT实验中观察到的平均上限）。结果显示，在O-S任务上，FCT与ACT表现相当，但在更复杂的-O任务上，ACT明显优于FCT。
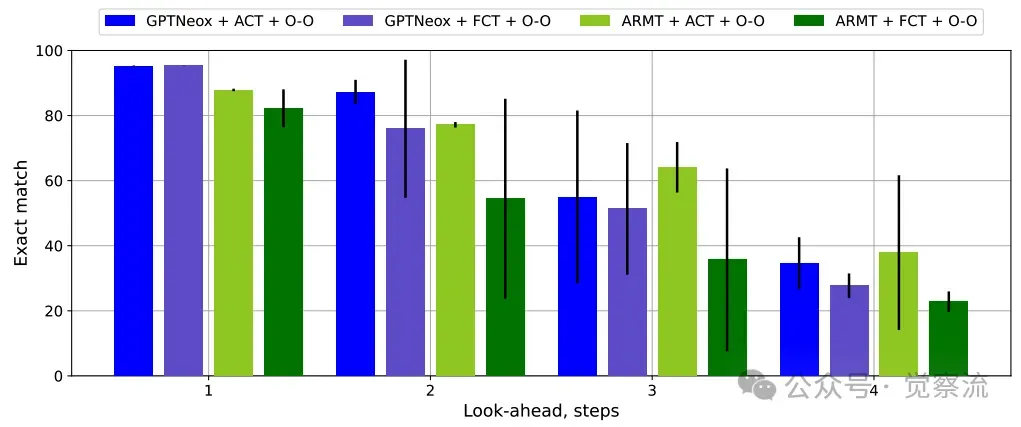
固定计算步数(FCT)在Orbit-Orbit任务中表现不佳
这说明ACT的智能之处在于它能"按需分配"计算资源，避免在简单样本上浪费算力，从而在整体上实现更优的效率-性能平衡。
策略三：强化学习"自省" (GRPO) —— 无监督扩展深度的革命性突破
如果说前两种策略是"工程师"的智慧，那么GRPO（Group Relative Policy Optimization）则展现了"进化论"的力量。在完全没有中间步骤监督的情况下，研究者仅通过最终答案的正确与否作为奖励信号，利用强化学习训练模型。
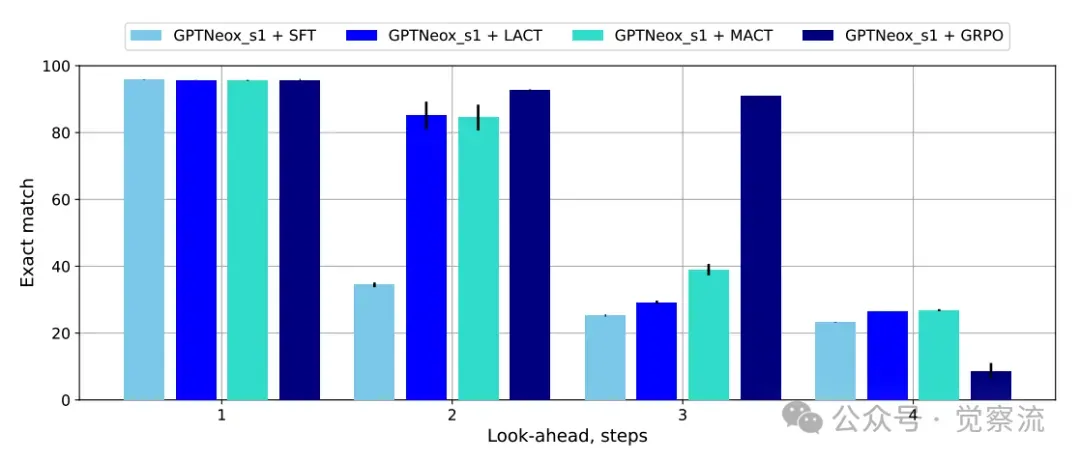
无监督RL训练使模型推理深度扩展至k=3
结果令人震惊：模型学会了在输出最终答案前，自回归地生成一系列内部的"思考"Token。通过这种方式，它成功地将推理深度扩展到了 k=3，其性能（约40%）甚至可以媲美有监督情况下的 k=2 任务。
这一发现为何具有革命性意义？ 它挑战了"显式中间表示是深度推理唯一可靠途径"的固有认知，证明了模型可以在无监督的条件下，自发地学会"内部思考"以增加推理深度。仅凭最终答案的奖励信号，就足以引导模型发展出复杂的、多步的内部推理过程，为未来无监督、自适应的推理能力涌现开辟了全新的道路。这表明，推理能力的涌现可能不需要人类精心设计的CoT提示，而是可以通过简单的奖励机制自然演化出来。
策略四：链式思维监督 (Chain-of-Thought - CoT) —— 可靠但昂贵的终极方案
当有充足的中间步骤监督信号时，CoT（Chain-of-Thought）训练展现出了无与伦比的可靠性。
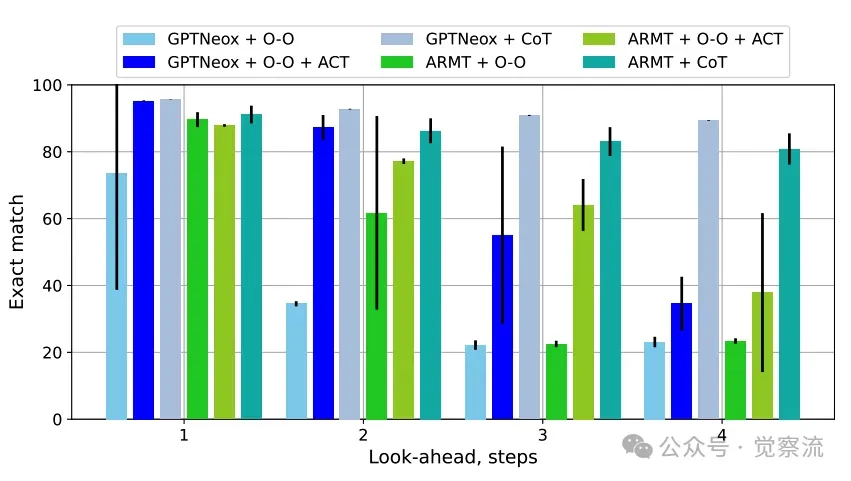
CoT方法在有监督情况下显著优于基于深度的ACT方法
在这种范式下，复杂的多步预测任务被分解为一系列简单的自回归单步生成任务。无论是GPTNeox还是ARMT，经过CoT训练后，都能在 k=4 的任务上达到接近100%的准确率。这无可辩驳地证明了，对"状态传播"过程的直接监督，是实现深度泛化的最可靠途径。
然而，这种可靠性是有代价的： 它依赖于昂贵且难以获取的中间步骤标注数据，并且在推理时会生成大量额外的Token，带来显著的计算开销，是一种"重装上阵"的解决方案。值得注意的是，单纯使用O-O任务（即并行预测所有中间状态）进行训练，效果并不理想，其性能甚至低于O-S任务。只有当O-O与ACT结合，或者升级为真正的、自回归的CoT训练时，性能才得到质的飞跃。这表明，顺序推理比并行推理更能有效模拟人类的思考过程。
超越语言——在群乘法任务上的普适性验证
为了验证上述发现在更广泛场景下的普适性，研究者在"群乘法"基准上进行了补充实验。之所以选择这个基准，是因为其计算本质与1dCA高度相似：都需要模型在内部维护一个"状态"（当前累积乘积），并根据输入序列中的新元素，按特定"规则"（群运算）反复更新这个状态。 这种同构性，使得我们可以将"序列长度"直接类比为1dCA中的"推理深度k"，从而在一个完全不同的任务上，复现并验证关于模型深度、循环和动态计算的核心发现。
该任务要求模型计算一个序列中所有元素的累积乘积，其计算复杂度随序列长度（即推理深度）线性增长。实验结果与1dCA基准高度一致。
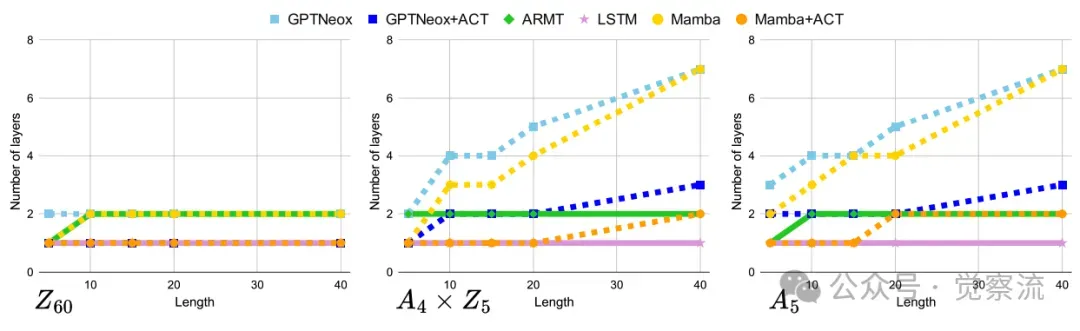
ACT显著降低模型解决群乘法任务所需的深度
Transformer和Mamba这类被理论证明为"TC0-limited"的模型，需要随着任务长度（深度）的增加而线性增加其层数，才能维持70%以上的准确率。相比之下，ARMT和LSTM凭借其内在的循环特性，能够以恒定的层数（仅需1-2层）解决任意深度的任务，再次彰显了循环架构在参数效率上的巨大优势。
更引人注目的是，为Transformer添加ACT，也能显著降低其所需的层数，部分缓解了深度瓶颈，这进一步证明了动态计算策略的广泛适用性和价值。例如，在A5群上处理长度为40的序列，标准Transformer可能需要8层以上，而添加ACT后，4层即可胜任。这一结果与1dCA基准中的发现完美呼应，证实了这些策略在不同任务中的普适性。
效率、架构与训练
现在，让我们回到最初的问题：神经网络如何真正"推理"？这项研究给出了清晰而深刻的答案。
首先，论文明确区分了推理的两个本质阶段：规则抽象与多步状态传播。 在1dCA基准中，所有模型都能高效完成规则抽象（k=1时准确率>95%），但当需要多步状态传播（k≥2）时，大多数模型性能急剧下降。这表明，规则抽象相对容易，而多步状态传播才是真正的瓶颈。正如论文中所说："规则抽象可以从有限观察中完成，但状态传播需要模型在内部维护和更新中间状态，这是一个更复杂的计算过程。"
其次，论文揭示了模型深度与宽度对推理能力的不同影响。 在神经网络中，宽度指每层神经元数量（d_model），深度指网络层数。
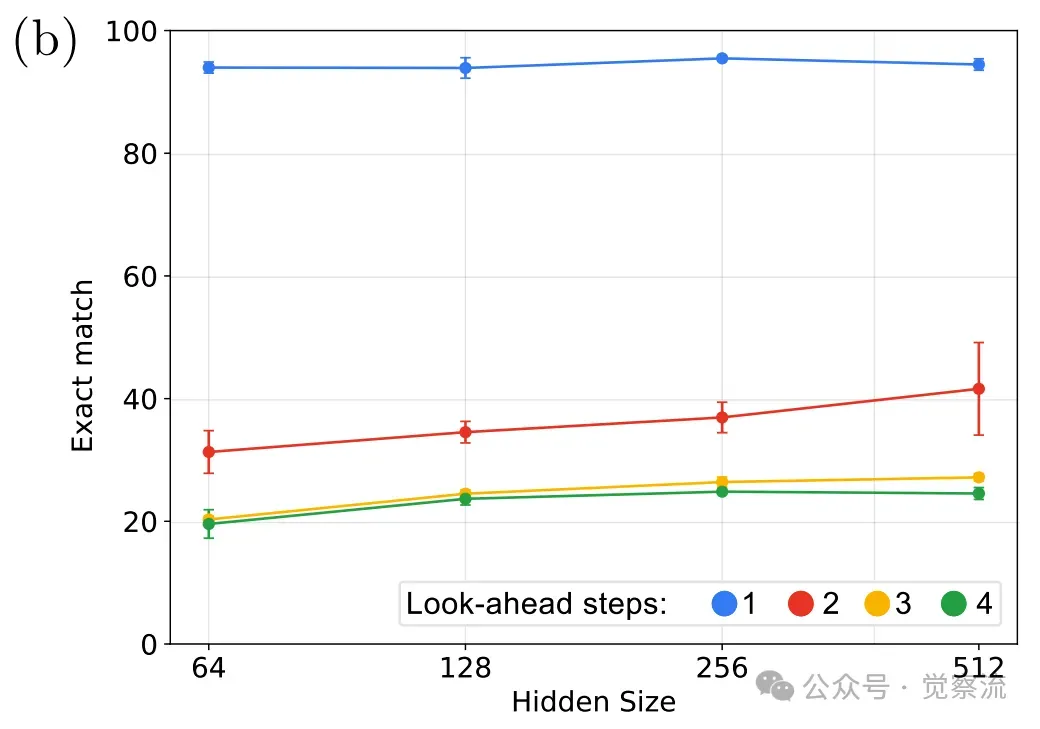
上图显示，增加宽度对多步推理能力的提升有限，特别是在达到128维度后，继续增加宽度收益甚微。而下图则显示，增加深度能显著提升多步推理能力：从4层增加到6层，k=2的准确率从约40%跃升至80%以上；增加到12层，k=3的准确率也能提升至约60%。
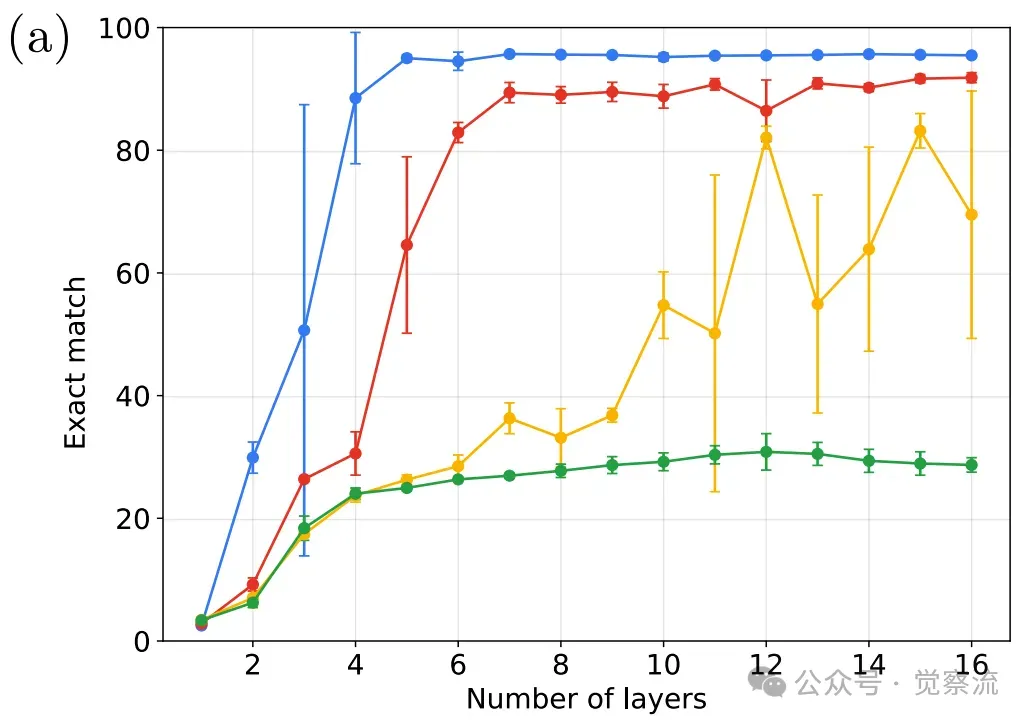
所以：推理能力不仅与模型宽度相关，层数的深度更为关键，特别是在需要多步推理的任务中。
第三，论文证明了"固定深度是难以逾越的硬约束"。 一个4层的模型，即使在单步推理上表现完美，也难以可靠地完成两步以上的推理。这解释了为什么LLM在奥赛中表现优异——这些任务往往可以被分解为一系列单步决策，而非真正需要多步规划的复杂问题。
那么，如何突破这一硬约束？论文提出了三种高效策略：
1. 循环架构（如ARMT）：通过分段级别的循环，强制模型分离规则与状态表示，使4层模型能处理k=2任务。这是一种参数高效的方案，因为它在不增加静态参数的情况下扩展了有效深度。
2. 动态计算（如ACT）：通过测试时的自适应计算，为Transformer等模型提供约"+1步"的额外推理能力。这是一种计算高效的方案，因为它只在需要时才增加计算量。
3. 无监督强化学习（如GRPO）：让模型通过强化学习自发生成"思考"Token，将推理深度扩展到k=3。这是最具革命性的发现，因为它证明了模型可以在没有中间监督的情况下学会"内部思考"。
最后，论文指出，有监督的链式思维（CoT）是目前最可靠的深度推理方案，但它需要昂贵的标注成本和计算开销。 当有中间步骤监督时，模型能轻松达到k=4的近100%准确率，这再次证明了显式中间表示对深度推理的关键作用。
再总结一下，这项研究告诉我们：
- 神经网络的"推理"能力有其根本限制，主要体现在多步状态传播上
- 固定深度是难以逾越的硬约束，增加宽度效果有限，增加深度有效但成本高昂
- 循环、动态计算和强化学习提供了在不增加参数前提下扩展有效推理深度的高效路径
- 规则抽象相对容易，但多步状态传播才是真正挑战，也是未来研究的关键方向
LLM的"思考"不应是一个黑箱。 这项研究为我们提供了一把精密的"解剖刀"——1dCA基准，它让我们得以清晰地看到：真正的深度推理，是"规则抽象"与"状态传播"的双重作用，而后者往往是无声的瓶颈。 通往"深思熟虑"的AI之路，不是无休止地堆砌参数，而要如何用循环的巧思、动态的智慧和训练的魔法，在有限的"脑容量"内，激发出无限的"思考深度"。
回到文章开头的那个问题：LLM在奥赛上的胜利，是真正的推理吗？基于1dCA基准的研究给出的答案是复杂的。在单步决策上，它们无疑是大师级的。但在需要多步规划、状态追踪的深层推理上，它们的表现急剧衰减，除非我们人为地为其增加深度、引入循环或提供详细的中间指导。
最终的胜利，将属于那些能在架构的巧思、训练的智慧与计算的效率之间，找到完美平衡点的探索者。 因为推理时，深度不是目的，而是手段；效率才是通往真正智能的桥梁。正如1dCA基准所示范的，未来研究应设计能明确分离"规则推断"与"多步状态传播"的可控实验环境，以精准定位模型瓶颈。研究者应系统性地报告模型在不同推理深度（k=1,2,3,4...）下的表现，并注明所使用的模型参数量和计算开销，以全面评估其有效推理深度与效率。
自适应计算策略（如ACT）和无监督的推理扩展方法（如GRPO）是极具前景的Scaling方向，值得深入探索。毕竟，真正的智能不在于记住答案，而在于学会思考——即使在资源有限的条件下，也能找到通往答案的路径。
