
本研究由快手科技语言大模型团队完成,核心作者苏振鹏,潘雷宇等。快手语言大模型团队聚焦在基础语言大模型研发、Agent RL 等前沿技术创新等方向,积累务实的探索 AGI 的能力边界,并不断推进 AI 领域新技术和新产品的发展。此前,该团队已开源了 Klear-46B-A2.5B 和 Klear-Reasoner-8B 等模型,其中 Klear-Reasoner-8B 在数学和代码的基准测试上达到了同参数级别模型的 SOTA 效果。
在大语言模型的后训练阶段,强化学习已成为提升模型能力和对齐质量的核心范式。然而,在广泛采用的 off-policy 的训练范式中,更新当前策略的数据由旧的行为策略生成,导致分布漂移的问题的发生,这通常会将策略推至信任域之外,使强化学习的训练变得不稳定。
尽管 PPO 通过重要性采样的裁剪机制缓解了部分问题,但它仅能约束已采样动作的概率变化,忽略了未采样动作的全局分布漂移。为了应对这些挑战,快手研究团队提出了一种创新的熵比裁剪方法。该方法从全新的视角切入,通过约束策略熵的相对变化来稳定全局分布,为强化学习训练提供了更加可靠的控制手段。

论文标题:Entropy Ratio Clipping as a Soft Global Constraint for Stable Reinforcement Learning
论文地址:https://arxiv.org/pdf/2512.05591
研究背景
强化学习训练过程中长期面临信任域偏离的挑战。目前,业界用于大模型的强化学习常采用 off-policy 训练范式,用于更新当前策略的数据由旧的行为策略生成,导致新旧策略之间存在分布漂移。主流方法通常采用重要性采样来纠正此类偏差,但其固有的高方差可能导致更新步长不稳定,仍存在信任域偏离的风险。这种偏离具体表现为训练过程中梯度范数和策略熵的剧烈波动。
PPO 算法是解决信任域偏离问题的主流方案,主要有两种形式:
PPO-penalty:在目标函数中加入 KL 散度惩罚项,对新旧策略的分布差异进行全局约束。但是惩罚系数非常敏感,且对每个动作概率施加逐点约束可能会抑制探索。
PPO-Clip:通过将重要性采样比率限制在固定区间内,形成局部信任域,裁剪过大的更新以降低方差。该方法更鲁棒且易于调参,但其约束仅作用于已采样的动作,未采样的动作则完全不受约束。
随着训练迭代的不断进行,这部分未受约束的动作分布会持续漂移,最终威胁策略的稳定性。例如,假设动作空间为 {a, b, c, d},旧策略的概率分布为 {0.85, 0, 0.15, 0},经过多次迭代后,新策略的概率分布变为 {0.82, 0.064, 0.07, 0.046}。尽管采样动作 a 的概率变化微小,PPO-Clip 不会触发裁剪,但其余动作的分布已发生显著偏移。
ERC 机制:从全局视角稳定策略分布
受 PPO-clip 启发,论文提出了熵比裁剪(ERC)机制,当新旧策略间的熵变化超出允许范围时,ERC 直接对样本梯度进行截断。ERC 并非取代 PPO-Clip,而是对其形成补充:PPO-Clip 仅约束采样动作的局部更新幅度,而 ERC 将熵比限制在一个适中的区间内,从而缓解整体策略分布的漂移。
首先,论文提出了熵比指标,其被定义为新旧策略在同一 token 上熵的相对变化。具体的,它被形式化定义为下式:
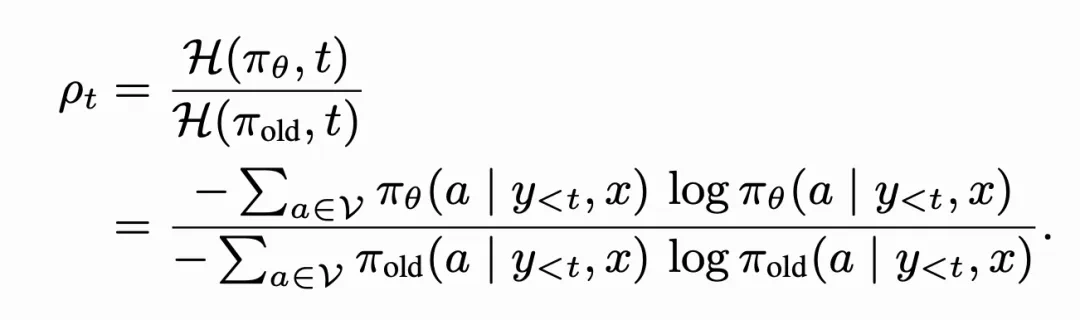
不同于重要性采样比率,熵比可以测量整个动作分布(包括未采样动作)的变化,提供了对策略全局漂移的度量。另外,论文还对采样动作概率与熵比的关系进行可视化,如下图所示:
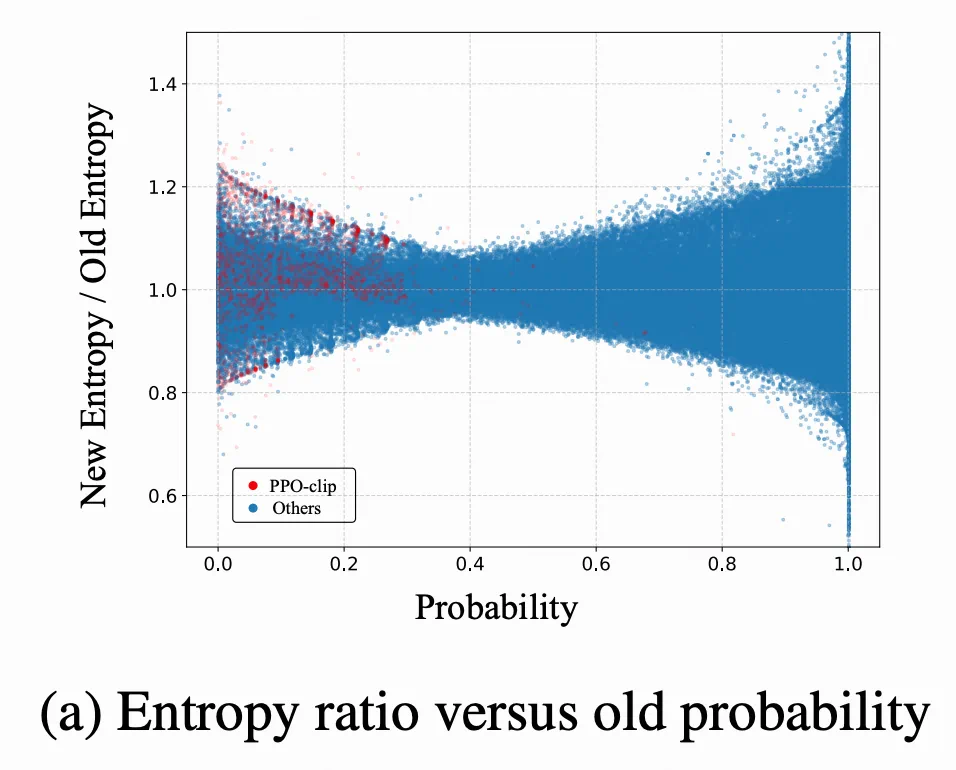
当采样动作较低或者较高时,全局分布偏移变得更加明显。
在将熵比作为策略分布的全局变化指标引入后,论文进一步将其集成到现有强化学习目标中,旨在约束新旧策略之间全局分布的变化。以 DAPO 为例,其 ERC 目标可形式化如下:
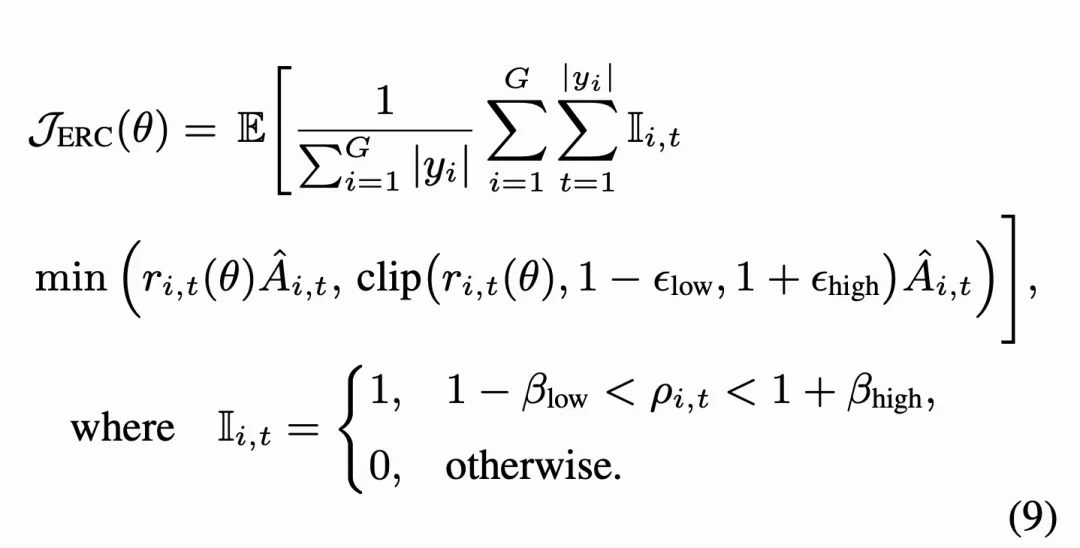
如果某个 token 的更新导致熵比超出预设范围,ERC 会直接截断其对应的梯度,以防止全局分布和策略熵的剧烈波动。与在整个训练过程中持续限制策略的 KL 约束不同,熵比仅在新策略的熵发生显著偏离时才被激活。这种方法既能防止策略分布的突然崩溃,又保留了足够的探索能力。
实验结果
为验证 ERC 方法的稳定性和性能上的有效性,论文在多个数学推理基准上进行了系统实验,包括 AIME24、AIME25、HMMT25、MATH500 、AMC23 和 Olympiad。所有实验均基于 DeepSeek-R1-Distill-Qwen 模型(1.5B 与 7B)进行训练。实验结果如下表所示。
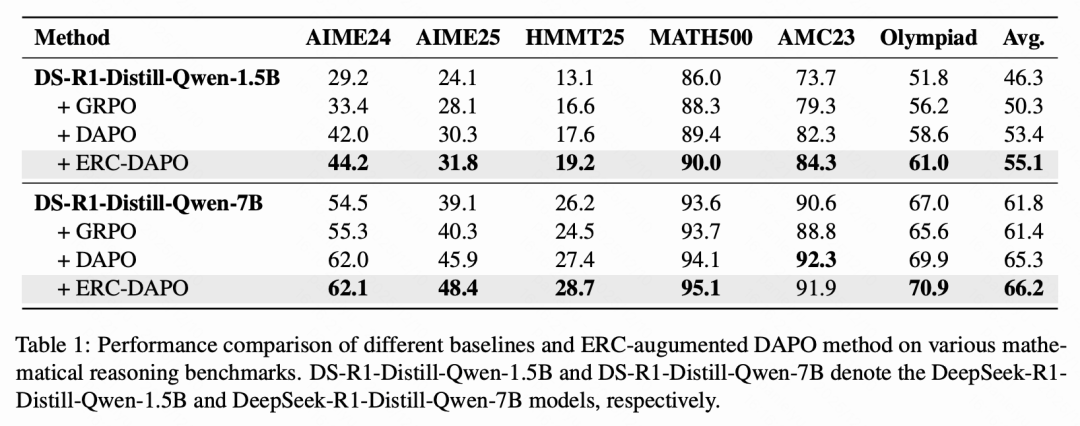
与现有的 RL 基线方法相比,集成 ERC 后,模型几乎在所有基准测试上的性能都得到了一致提升。值得注意的是,在 AIME25 和 HMMT25 等更具挑战性的基准上,性能增益更为显著,凸显了 ERC 在复杂推理场景中的强大潜力。此外,该方法在 1.5B 和 7B 两种参数规模上均取得了一致的改进,进一步证明了其在不同模型容量下的鲁棒性和可扩展性。
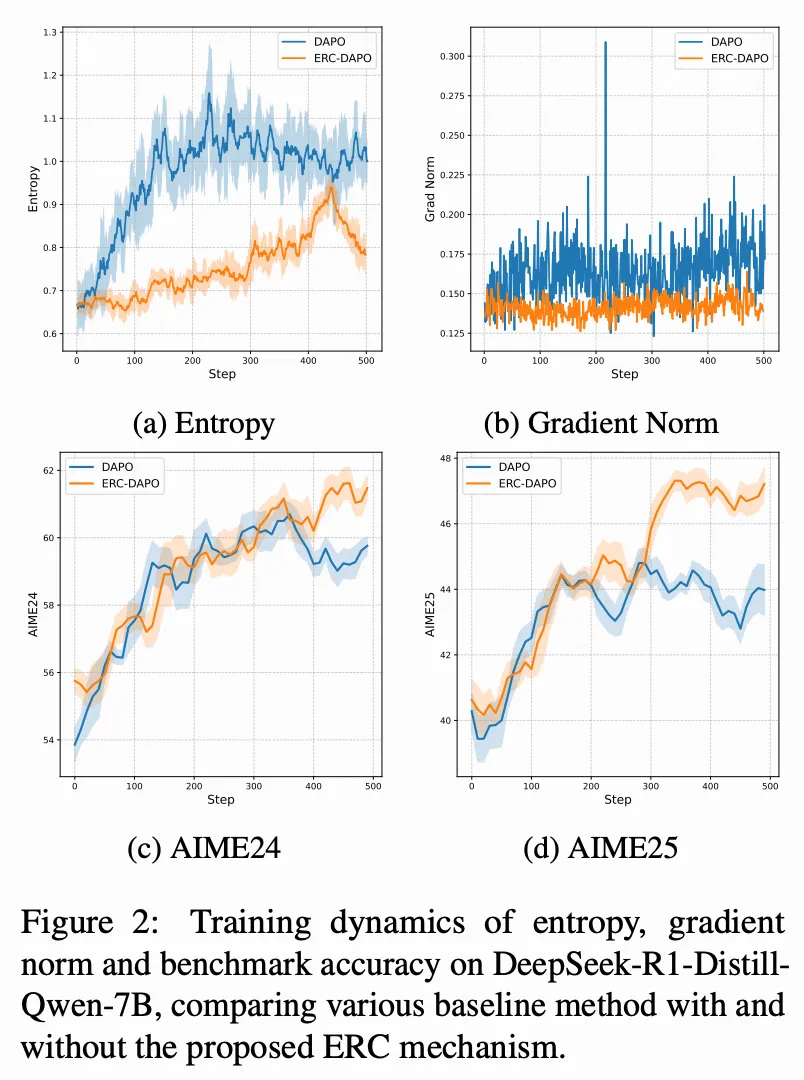
为了进一步验证 ERC 对训练动态的影响,论文比较了不同方法下熵和梯度范数的演化过程,如上图所示。传统的裁剪方法在训练过程中常表现出较大的熵值波动和不稳定的梯度。相比之下,ERC 引入了全局熵比约束,熵值轨迹和梯度范数更加稳定,在基准上的评测结果也不断提升。
深入分析:ERC 如何工作?
增强信任域约束
如下图所示,ERC 的裁剪机制有效地强化了信任域约束。具体而言,被熵比边界裁剪的 token 主要位于信任域的边界附近。这表明,ERC 从全局分布的视角出发,能够识别并限制可能导致策略偏离的更新,而这些更新正是 PPO-Clip 的局部约束所忽略的。因此,ERC 与 PPO-Clip 以互补的方式协同工作,共同减轻信任域偏离,增强训练稳定性。
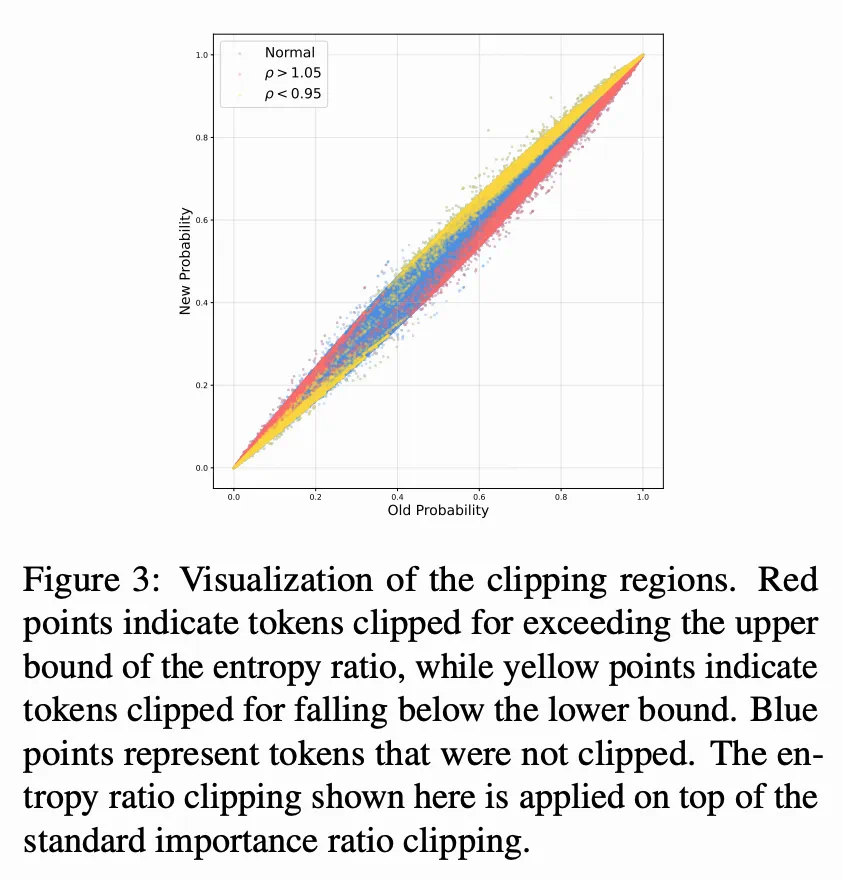
通过 ERC 保持探索
为了理解 ERC 对模型探索行为的影响,论文分析了在训练中被熵比约束裁剪的 token 的熵分布,如下图所示,大多数被 ERC 裁剪的 token 集中在低熵区域,而高熵 token 在优化过程中通常被保留。这表明 ERC 优先抑制那些过于确定性、信息增益有限的 token 的更新,而不会过度约束模型的探索动态。
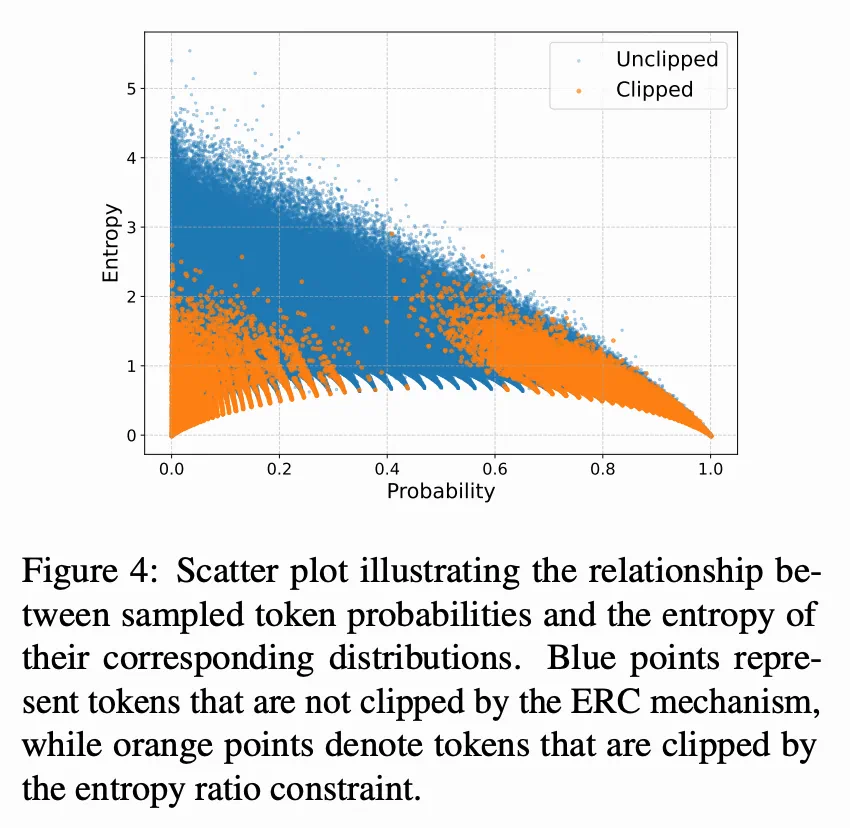
裁剪比例分析
实验结果显示,ERC 引入的全局分布约束显著提高了裁剪比例。PPO-Clip 下的裁剪比例通常保持在 0.02% 左右,而 ERC 将此数值提高了近三个数量级,达到约 20%。这种显著差异源于两种约束机制的根本不同:PPO-Clip 仅调控局部采样动作的重要性比率,越界情况本就罕见;而 ERC 超越了这种局部约束,通过熵比融入了全局分布信号,使其能够识别并裁剪大量在全局分布层面偏离信任区域的 token 更新。
尽管 ERC 的裁剪比例显著更高,但其在最终性能和训练稳定性上均持续超越 PPO-Clip 基线。这个看似违反直觉的结果揭示了一个关键见解:ERC 主要移除了那些会使训练不稳定的噪声更新。被 ERC 裁剪的 token 大多集中在低熵区域,这表明 ERC 抑制了过于确定性且可能有害的更新,同时保留了模型在其他地方的探索行为。
对比与泛化能力
论文还将 ERC 与其他稳定方法进行了对比,并验证了其在其他强化学习算法中的泛化能力。
与 KL 正则化的对比:ERC 在 AIME24 和 AIME25 基准上均优于 PPO-penalty(即 KL 正则化方法)。KL 散度施加的是逐点约束,要求新旧策略对每个动作的概率分布都保持接近,这种严格的局部调控虽然可以稳定训练,但不可避免地限制了有效的策略探索。而 ERC 实现了分布层面的软约束,通过监控熵比来关注整体策略分布的演变,在维持训练稳定性的同时鼓励更高效的探索。
与熵正则化的对比:ERC 的表现显著优于在强化学习训练中直接加入熵惩罚项的方法。熵正则化只能缓解单向的不稳定性(熵崩塌),而 ERC 的双向裁剪机制能有效应对策略演化中熵值波动的两个方向,确保策略的探索行为在合理可控的范围内平稳演变。
与序列级裁剪(GSPO)的对比:在 DeepSeek-R1-Distill-Qwen-7B 上的实验表明,结合了 PPO-Clip 和 ERC 的 token 级裁剪方法相较于序列级裁剪方法(如 GSPO)仍具有明显优势。值得注意的是,ERC 与序列级裁剪是正交的,可以同时使用。
更广泛的适用性:除了 DAPO,论文还将 ERC 与 GPPO 方法结合。实验表明,将 ERC 集成到 GPPO 中同样能带来一致的性能提升,为 ERC 在不同 RL 算法中的普遍有效性提供了有力证据。这表明 ERC 不仅是现有重要性比率裁剪技术的补充组件,也有潜力作为一个独立且鲁棒的约束机制来稳定策略优化。



