本文第一作者是西湖大学博士生冯睿骐，通讯作者为西湖大学人工智能系助理教授吴泰霖。吴泰霖实验室专注于解决 AI 和科学交叉的核心问题，包含科学仿真、控制、科学发现。
在解决离线强化学习、图片逆问题等任务中，对生成模型的能量引导（energy guidance）是一种可控的生成方法，它构造灵活，适用于各种任务，且允许无额外训练条件生成模型。同时流匹配（flow matching）框架作为一种生成模型，近期在分子生成、图片生成等领域中已经展现出巨大潜力。
然而，作为比扩散模型更一般的框架，流匹配允许从几乎任意的源分布以及耦合分布中生成样本。这在使得它更灵活的同时，也使得能量引导的实现与扩散模型有根本不同且更加复杂。因此，对于流匹配来说，如何得到具有理论保证的能量引导算法仍然是一个挑战。
针对这一问题，作者从理论上推导得到全新能量引导理论框架，并进一步提出多样的实际能量引导算法，可以根据任务特性进行灵活选择。本工作的主要贡献如下：
- 本工作首次提出了流匹配能量引导理论框架。
- 在本框架指导下，本工作提出三大类无需训练的实用流匹配能量引导算法，并可将经典扩散模型能量引导算法包含为特例。
- 本工作给出了各个流匹配能量引导算法性能的理论分析和实验比较，为实际应用提供指导。
- 论文标题：On the Guidance of Flow Matching
- 论文链接：https://arxiv.org/abs/2502.02150
- 项目地址：https://github.com/AI4Science-WestlakeU/flow_guidance
目前，本工作已被接受为 ICML 2025 spotlight poster，代码已经开源。
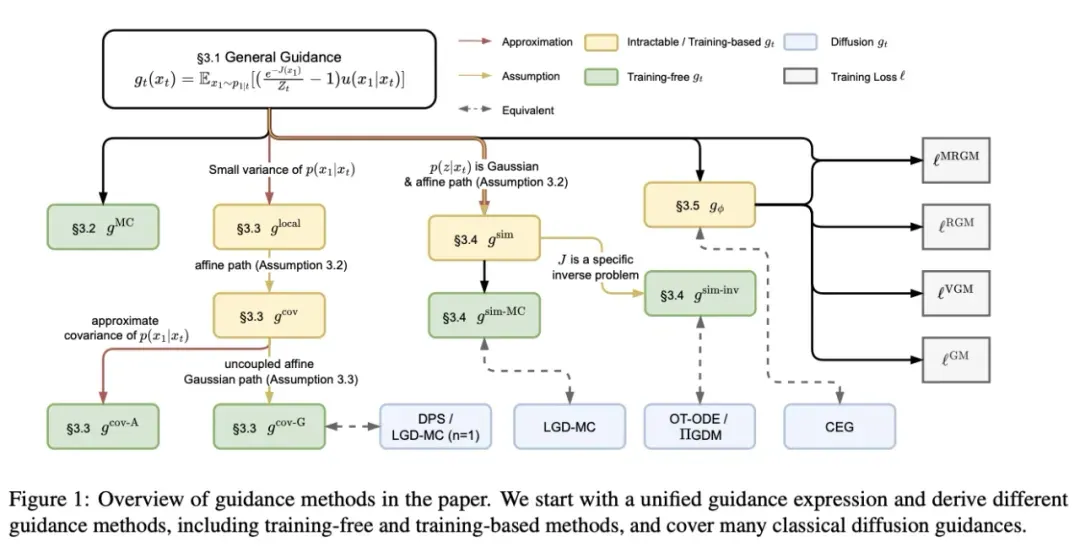
研究背景
在生成模型的应用中，能量引导是一种重要的技术。理想情况下，它通过在模型已有的向量场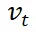
中加上一个引导向量场
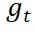，使生成的样本服从的分布从训练集分布
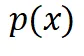改变为被某个能量函数
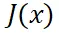加权后的分布
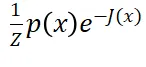。这样一来，通过将能量函数设置为可控生成中的目标函数，即可使生成的样本同时符合训练集和满足目标。
已有的能量引导算法集中于扩散模型，但是流匹配模型和扩散模型相比有本质上的差别，使得它们的能量引导算法不能直接通用。简而言之，扩散模型可以被看作是流匹配模型在这些假设下的特例：源分布是高斯分布、源分布和生成分布之间没有耦合、条件速度场满足特定的线性形式。
在这些假设下，扩散模型的向量场可以和得分函数（score function）关联起来，从而能量引导向量场可以被大大简化，成为能量函数对数期望的梯度形式。在没有这些假设时，能量引导向量场则需要几乎完全重新推导。
目前虽然已经有一些工作对流匹配模型进行能量引导，但是这些流匹配模型仍然采用了高斯源分布等三个假设，所以本质上仍然是扩散模型（仅有条件向量场的系数中有细微不同）。因此，一个具有一般性的流匹配能量引导理论框架是必要的。
方法概述
首先，作者从流匹配模型基础定义出发，推导了一般的流匹配能量引导向量场。具体而言，将叠加了能量引导后的总向量场与原向量场相减，
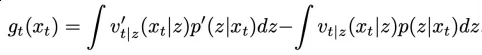
其中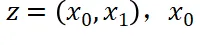
是源分布样本，
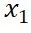是目标分布样本。经过化简即可得到，
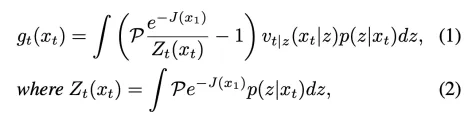
其中在实际数据集中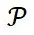
可以近似为 1。
直观上来说，引导向量场在能量函数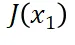
小于它的平均值时将指向对应的
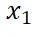，从而将原向量场转向能量函数更小的区域。为了实现实际的能量引导，作者接下来提出三大类不同的无需训练的能量引导算法。
蒙特卡洛估计
在引导向量场的计算中，主要困难来源于从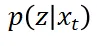
中采样。通过使用重要性采样（importance sampling）技术，可以将从这一分布中采样转化为从更简单的
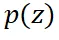中采样。从
中采样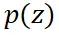，只需从训练数据集中采样（如果可用），或者使用原模型生成服从
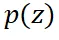的样本。
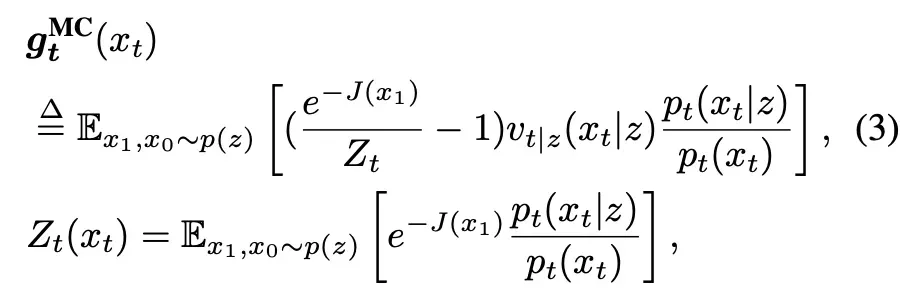
利用这一方法，在样本数不限的情况下可以计算精确的能量引导向量场。
梯度近似
为了更高效地计算引导向量场，可以通过近似来得到更简单的形式。一个直接的近似是利用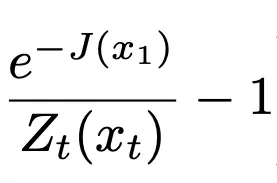 
在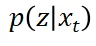
分布的均值附近的泰勒展开，通过只保留一阶项来化简。计算可得
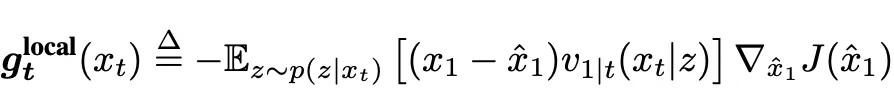
也就是得到了扩散模型引导向量场中常见的「能量函数的梯度」的形式。注意到梯度前面的项和能量函数无关，可以进一步通过设置成超参数来近似，或者在一些特殊情况的流匹配模型中，可以被进一步简化。
例如，通过采用源分布是高斯分布、源分布和生成分布之间没有耦合、条件速度场满足特定的线性形式的假设（即和扩散模型相同），可以简化为经典的扩散后验采样（Diffusion Posterior Sampling, DPS）算法。
值得注意的是，虽然在扩散模型的特例中，最终形式和 DPS 相同，但是推导方式截然不同。DPS 基于扩散能量引导框架，利用 Jensen 不等式来消除不可计算的期望，但这里基于流匹配能量引导框架，则是使用泰勒展开来简化这一期望的计算。
流匹配框架不仅提供了一个替代的理论理解视角，而且从中可以导出引导向量场的误差上界。该误差和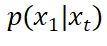
的协方差矩阵（代表着当前噪声样本可以多准确地估计最终生成的干净样本），以及
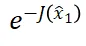的 Hessian（代表着能量函数变化多剧烈）有关。
高斯近似
由于从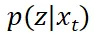
中采样困难，还可以直接假设
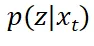是一个可以采样的简单分布，例如高斯分布。只需要将该高斯分布的均值和方差设置为和
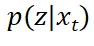一致（甚至方差可以简单设置为一个超参数），就可以期待从该高斯分布中采样估计的引导向量场和真实引导向量场接近：
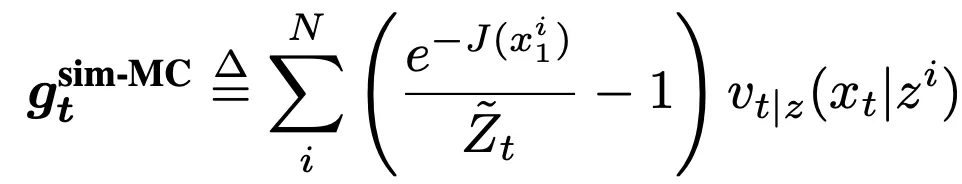
更进一步地，如果考虑具体任务中，能量函数的特定形式，比如含有高斯噪声的线性逆问题中，
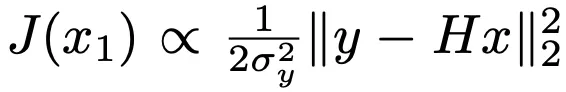
那么在该高斯近似下，可以计算引导向量场的解析表达式。
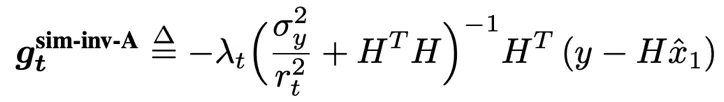
事实上，这和经典的伪逆引导扩散模型（GDM）的形式高度相似，在选取扩散模型对应的去噪进度超参数后可以完全简化为 GDM。
实验结果
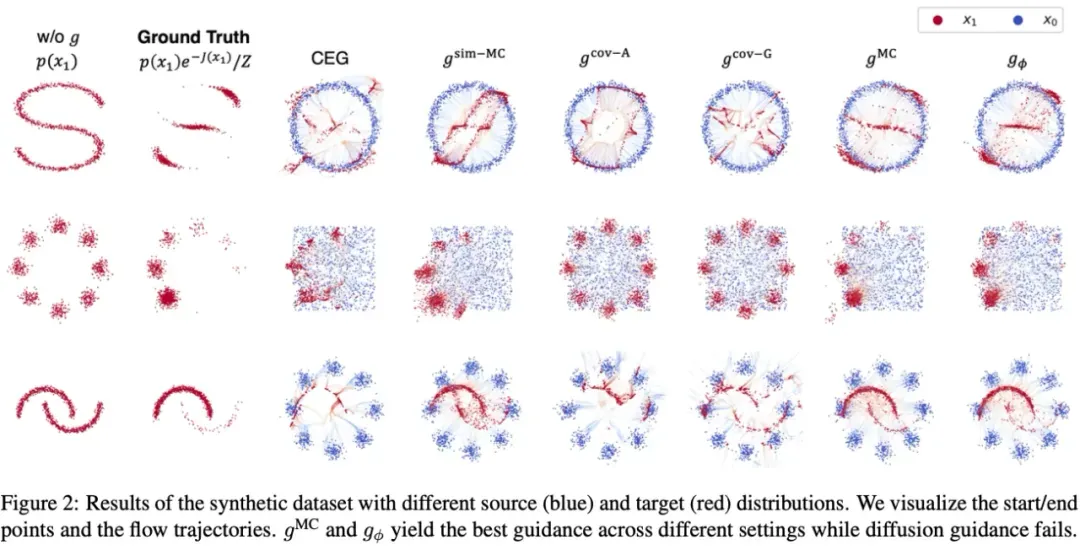
作者在合成数据、离线强化学习和图片线性逆问题中进行了实验。首先，在合成数据集上进行实验。源分布被设置成图中左一列的非高斯分布，并且能量函数包含简单表达式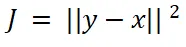
（第一行）、关于极坐标下极角的阶梯函数（第二行）、MLP 分类器的输出（第三行）。
这些流匹配引导任务和扩散模型显著不同，因此针对扩散模型的精确能量引导方法（左三列，对比能量引导 CEG）完全失败。同时基于蒙特卡洛采样的引导算法取得了最接近真实（ground truth）分布的结果，佐证了它是渐进精确的和流匹配引导框架的正确性。
此外，为了从实验上比较各个引导算法优劣，作者还在离线强化学习（offline RL）和图片线性逆问题任务中测试了各个引导生成算法的效果，结果如表所示。
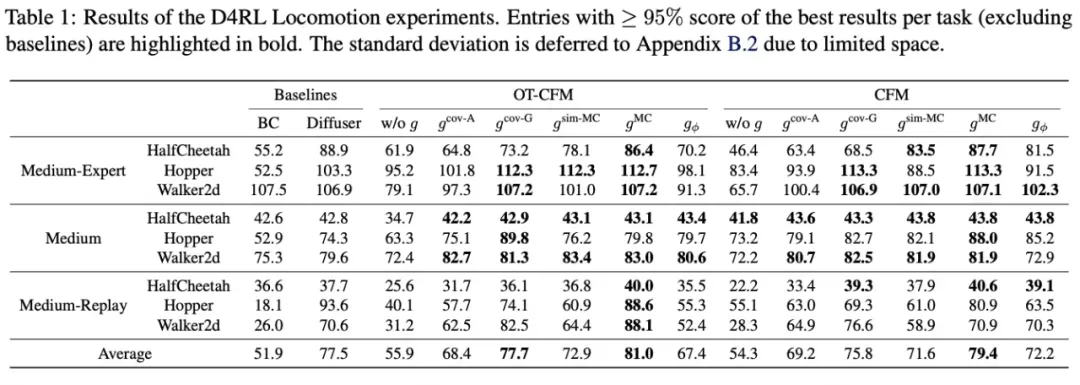
总体来说，在离线强化学习任务中，蒙特卡洛采样引导有最佳性能。这可能由于离线强化学习任务中需要同一个引导算法在不同时间步的条件下都产生稳定的引导采样样本，因此理论保证的能量引导算法具有最佳性能；而图片逆问题中，针对此逆问题形式设计的高斯近似引导和 GDM 有最佳性能，而蒙特卡洛采样引导由于问题维度较高不能产生合理的引导向量场。
结论
本工作针对流匹配模型中能量引导算法的空白，提出了一种新的能量引导的理论框架，并且提出几类各有优劣的实用引导算法，适用于一般的流匹配模型。此外，通过理论分析和实验对各个引导算法进行了比较，提供了实际应用指导。本工作希望为流匹配引导采样和为生成模型的进一步应用提供理论基础。
