
作者丨陈天宇
编辑丨ScienceAI
而偏微分方程(PDE),正是这本著作中最核心的篇章之一。它刻画了从量子涨落到星系演化,从流体冲击到电磁传播的普适物理规律。然而,求解 PDE 却如同破译大自然的密码,传统数值方法计算昂贵,专用神经网络模型则局限特定问题,一个模型通常只能求解一种维度、一类物理量、特定边界条件的方程。面对真实世界多尺度、多物理场强耦合的复杂系统,人们不得不为每个子问题「量身定制」求解器,知识无法迁移与复用,模型也难以通过数据和参数进行规模扩展。「大自然的书籍是用数学语言写成的。」 —— 伽利略
能否像 ChatGPT 理解语言一样,构建一个理解并求解「物理语言」的通用基础模型?
近期,北京航空航天大学李建欣教授团队提出了科学智算基础模型 OmniArch,首次实现单个模型统一求解 1D、2D、3D PDE 的重大突破,并在多个关键指标上大幅超越现有方法。相关成果以《OmniArch: Building Foundation Model For Scientific Computing》为题,被 ICML 2025 接收。

论文地址:https://openreview.net/pdf?id=UlprLwWYKP
代码地址:https://openi.pcl.ac.cn/cty315/OmniArch
CNAI4S 科学智算共性平台:https://cnai4s.com/
挑战:阻碍「物理 GPT」-OmniArch 的三座大山

构建面向 PDE 求解的通用基础模型,需跨越三大核心障碍:
1. 多维度统一表示:物理数据形态各异(1D 序列、2D 场、3D 体),传统架构需为不同维度设计专门网络,知识难以共享。
2. 多物理量统一处理:不同 PDE 包含的物理量数量迥异(如流体方程含速度/压力/密度,电磁方程有 6 个分量)。统一模型需能动态处理变化的物理量组合及其复杂相互作用。
3. 物理约束对齐:每个 PDE 都蕴含各自的「物理法则」(守恒律、边界条件、对称性)。基础模型如何在保持灵活性的同时,自适应地满足这些严格约束,确保解的物理合理性?
OmniArch:统一架构的三大创新突破
OmniArch 创造性地融合了频域变换、注意力机制与对比学习,攻克了上述难题:
1. Fourier编码器实现维度统一
尽管物理数据在欧氏空间维度不同,但在频域空间具有统一的多尺度结构。因此,OmniArch 对输入坐标和物理场进行快速傅里叶变换(FFT),保留最重要的 Top-K 频率分量(模式),从而将不同维度/分辨率的数据转换为统一长度的频域表示。
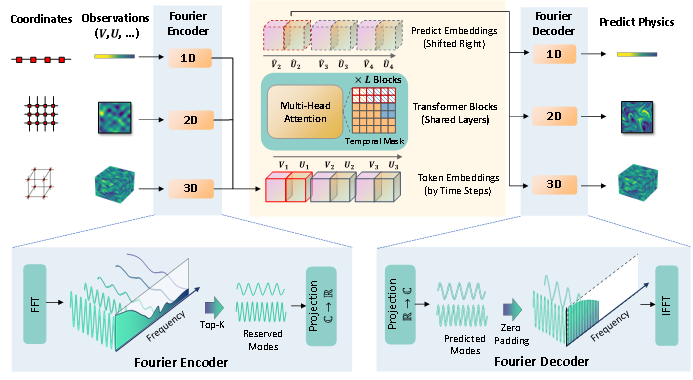
优势:(1) 计算效率从 O(N²)降至 O(NlogN);(2) 低频捕获全局模式,高频编码局部细节;(3) 不同分辨率数据在低频部分自然对齐。
2. Temporal Mask 实现多物理变量耦合
标准 Transformer 采用因果注意力机制,但这会破坏同一时刻物理量之间的相互作用。OmniArch 引入 Temporal Mask:
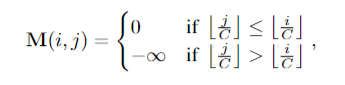
时刻内完全连接:同一时间步的所有物理量 token 可相互「看见」并交互,精确建模耦合关系(如 NS 方程中的速度-压力耦合)。
时刻间因果约束: 严格遵循时间序列因果性,未来状态不影响过去。
这种设计自然地编码了物理系统时序演进与瞬时耦合的核心特性。
3. PDE-Aligner 增强物理一致性
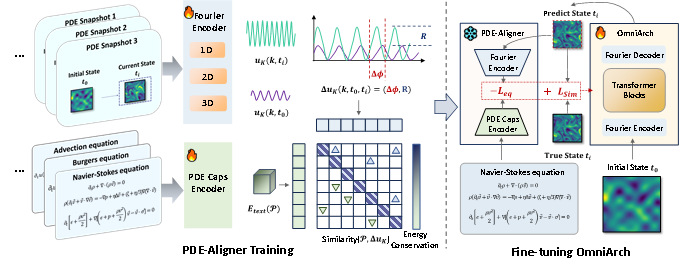
在微调阶段,PDE-Aligner 通过对比学习将符号方程与数值演化对齐:
方程编码:预训练 BERT 处理 LaTeX 格式的 PDE 文本
物理特征:频域相位差 Δφ 和振幅比 R 编码演化模式
能量约束:确保 ∑|R|≈1 满足 Parseval 定理
这种「软对齐」避免了硬编码物理约束,使模型能够自适应不同方程和边界条件的约束。
实验验证
OmniArch 在涵盖流体力学、电磁学、反应扩散等领域的 11 种经典 PDE 上进行了严格测试(数据集:PDEBench, PDEArena),对比了包括专用模型(PINNs, U-Net, FNO)和前沿统一预训练模型(MPP, Poseidon, DPOT, PDEformer-1)在内的众多基线。
1. 基准性能:精度飞跃,最高提升 98.7%
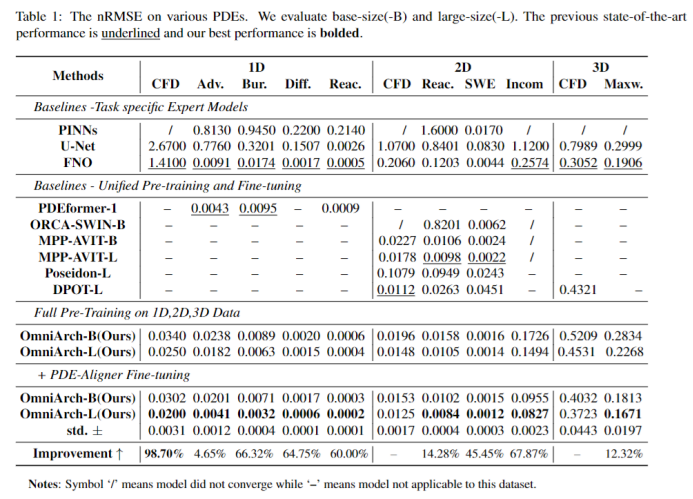
表:OmniArch 在 11 类 PDE 上的 nRMSE 性能对比(越低越好),显著优于专用模型(上)与其他统一预训练模型(中)。下划线为之前 SOTA,加粗为本文最佳。
One vs All:OmniArch(Base/Large 版本)在全部11项测试中均取得最佳或接近最佳性能。单个模型、单份权重即可全面替代针对不同维度、不同 PDE 专门设计的众多模型。
CFD 求解的显著优势:在最具挑战性的计算流体动力学(CFD)任务上,OmniArch 展现出较大优势,其中 1D CFD 方程求解相比最佳基线,误差降低 98.7%。
物理对齐效果:PDE-Aligner 微调带来平均超过 20% 的精度提升,证明了其有效注入物理知识的能力。
2. 零样本泛化:「举一反三」的物理直觉
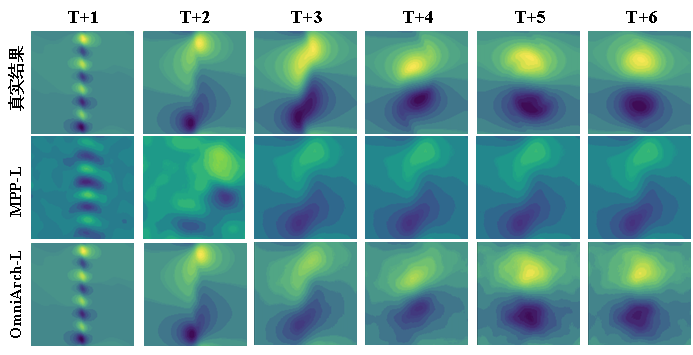
未见过的方程直接解:OmniArch 无需微调,即可对训练集之外的复杂 PDE 进行高精度求解。在 Shock(激波)、KH(开尔文-亥姆霍兹不稳定性)、OTVortex 等三个高难度 2D 流体物理系统上,其零样本性能显著超越了专门在这些任务上训练的 FNO、U-Net 模型。相比同样做预训练的 MPP-Large 模型,误差降低了 4-7 倍 (如 KH: 0.2763 vs. 1.3261)。
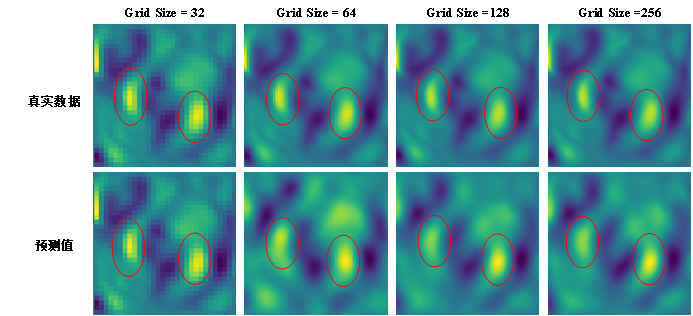
空间分辨率直接泛化:得益于频域表示的尺度不变性,OmniArch在训练(如128x128)后,无需修改架构即可直接处理截然不同的输入分辨率(32x32, 256x256, 512x512),且精度保持在可接受范围(nRMSE < 0.2),计算延迟几乎不变。这解决了传统方法因网格绑定需重新训练或插值的问题。
3. 上下文学习:动态「领悟」物理规则
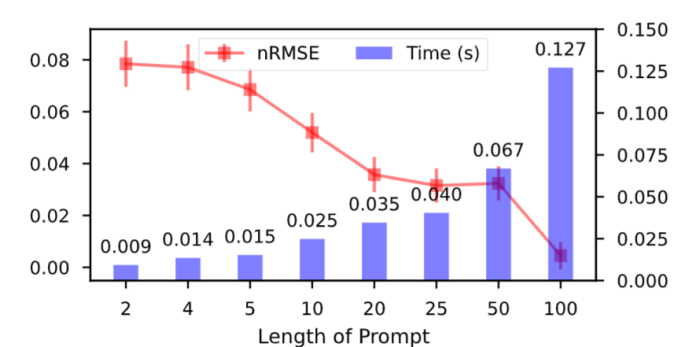
如同大语言模型(LLM)通过提示(Prompt)理解新任务,经过预训练的 OmniArch 展现出了上下文学习能力。给定少量历史时间步的观测数据(称为「PDE Prompt」),模型即可动态学习并模拟出该特定 PDE 的算子。
未来,团队计划将 OmniArch 拓展到更广泛的 PDE 类型、更复杂的边界条件,并探索其在气候模拟、航天航空器辅助设计等重大科学工程问题中的落地应用。
作者介绍
陈天宇,北航卓越百人博士后,研究方向包括科学智算 AI4S、大模型安全等交叉领域,发表 ICML、TIFS 等 CCF-A 类会议期刊论文 8 篇,获 CVPR 2025 亮点论文,受邀「AI+X」全国优博论坛等作报告,作为核心成员参与搭建 CNAI4S 科学智算共性平台,获 IJCAI 流体智算大赛 F 奖,工信部全国工业 APP 大赛冠军等。



