编辑丨%
量子计算听起来就很烧脑了，但在理论世界里还有一群人，他们专门研究「量子证明」能做到什么程度。这个领域叫量子复杂性理论，其中很出名的一个类是 QMA ——它是「量子版的NP问题」，可以理解成：有一个「量子证明」，由验证者用量子计算机来检查真假。
过去二十年，研究者不断尝试把验证错误率压得越来越低，就像玩游戏要刷「满暴击率」。而这次，理论物理学家 Scott Aaronson 和合作者 Freek Witteveen 给出了一个明确答案：用黑箱方法，你刷到头了。
他们的思路已经走到了尽头，因此转而寻求 GPT-5 的帮助。通过不断改进，该模型最终提出了一种巧妙的数学函数，使得可以精确分析特征值的行为。
相关的研究内容以「Limits to black-box amplification in QMA」为题发表在 arxiv。
论文链接：https://arxiv.org/abs/2509.21131
放大是什么？极限又在哪里？
我们先来见到了解一下什么是 NP 问题。在这里，它是所有决策问题的集合，对于这些问题的答案如果是「是」，则有 2/3 的概率被接收，反之则最多是 1/3。正如复杂性理论中通常所做的那样，2/3 和 1/3 只是惯例，可以用放大（例如）替换为 1-2⁻ⁿ 和 2⁻ⁿ 。
好吧，量子领域的相关知识着实令人头疼。就好比说在经典复杂性理论里，有一个常识：只要多跑几次验证，就能把出错概率降到很小很小。本来有 90% 把握，现在重复一百次取多数票，就能让把握接近 100%，这就叫放大（amplification）。
在量子世界里也类似，QMA 协议也能通过放大来提高「完整性」（正确证明被接受的概率）和降低「健壮性」（错误证明蒙混过关的概率）。 今年六月，Freek Witteveen 和博客的老朋友 Stacey Jeffery 就已经证明过：完整性可以被放大到 双指数级 接近 1。听起来很疯狂——比指数级还狠。
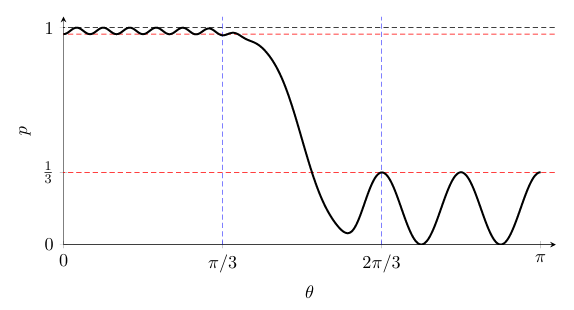
图示：对或然黑盒进行访问以决定θ ≤ π/3（是实例）或θ ≥ 2π/3（否实例）。
Scott 表示，在四分之一个世纪后仍能以一种从未想过的方法做到了这一点（其中接受的概率是通过量子态的幅度在几何级数中减小来编码），着实令他惊喜。不过，在此基础上是否可以更进一步？比如真的做到「100% 接受正确证明」？
但回答却是：不能，至少黑箱方法到此为止了。
使用黑匣子技术，双倍指数小完整性误差是能做的最好的事情。换句话说：Scott 表明，当人们将他的 2008 年 QMA ≠(QMA 1) 量子预言机分离定量化时，人们会得到一个与 Freek 和 Stacey 的协议完全匹配的下限。
就在这里，AI 出手了
写到这里，其实作者完全可以凭借自己与同伴完成这份工作（当然他也是这么认为的），但他还是尝试把其中的关键技术步骤交给人工智能——GPT-5。
五分钟之后，AI 给出了一堆看上去是对的但实际上逻辑根本不通的东西。不过好在作者知道哪里需要改进哪里需要纠错，就在这么半小时之后，AI 给出了一条建议：
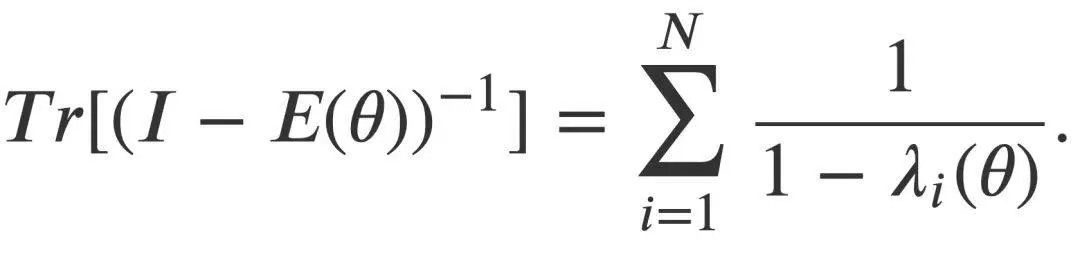
它正确地指出，这是一个关于 θ 的可控度有理函数，恰好编码了最大的特征值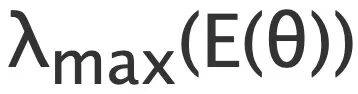
接近 1 的相关信息。而这……相当有效。作者表示，如果是他的学生提交了这个建议，他会觉得这个思路很巧妙。也许只是 AI 在训练数据中碰巧看到了这个或类似的构造。
关于这些，Scott 调侃道：目前，它可能还无法撰写整篇研究论文（至少如果你希望它正确且出色的话），但它可以帮助你摆脱困境。谁知道这种状态会持续多久呢？他想他应该感激自己拥有终身教职。
一些愉快的小讨论
技术上，作者们给出了定量版本的分离结果，把自己 2008 年的工作延伸到了今天。虽然这还不是解决「QMA 是否等于 QMA 1」的最终答案，但至少说明了某条路已经走到尽头。
他们留下的核心未解问题是，在部分或者所有有限门控集的影响下，QMA 是否可以等于 QMA 1。
另一个较小的问题开放性问题是，在算子分离中，是否可以取角度 θ 为一个固定的值，比如 θ = π，在无案例中，而不是属于一个值域。
猜测答案是肯定的，但似乎需要一个新的论据。
作者博客：https://scottaaronson.blog/?p=9183
相关链接：https://x.com/kimmonismus/status/1972399015825203463
