Zeju Qiu和Tim Z. Xiao是德国马普所博士生,Simon Buchholz和Maximilian Dax担任德国马普所博士后研究员,Bernhard Schölkopf是德国马普所所长,Weiyang Liu是香港中文大学计算机系助理教授。
随着大型语言模型(LLM)推动人工智能领域取得突破性进展,如何实现高效、稳定的超大规模模型训练,始终是该领域最富挑战性的核心议题之一。
针对这一关键问题,研究者们提出了一种基于第一性原理的全新方法——POET(Reparameterized Training via Orthogonal Equivalence Transformation),该方法通过重参数化优化策略,旨在从第一性原理出发提升训练效率与稳定性。

Paper:Reparameterized LLM Training via Orthogonal Equivalence Transformation
Project page:https://spherelab.ai/poet/
Arxiv:https://www.arxiv.org/abs/2506.08001
POET:基于第一性原理的大型语言模型全新训练范式
POET 的关键思想是:通过对每个神经元进行结构性重参数化,引入两个可学习的正交矩阵以及一个固定的随机权重矩阵,从而构建一个正交等价的变换结构。该方法在训练过程中严格保持权重的奇异值分布,并天然拥有较低的球面能量,这是 POET 有效性的核心来源。
通过联合建模奇异值不变性与最小超球能量,POET为大模型训练提供了一种兼具物理解释性与泛化能力的新范式。由于该方法严格保持权重矩阵的谱结构,不仅能稳定优化过程,还显著提升了模型的泛化性能。为兼顾计算效率与实用性,研究者还开发了高效的近似算法,使POET可扩展至超大规模神经网络训练。实验结果表明,该方法在大型语言模型训练中表现出卓越的性能与可扩展性。
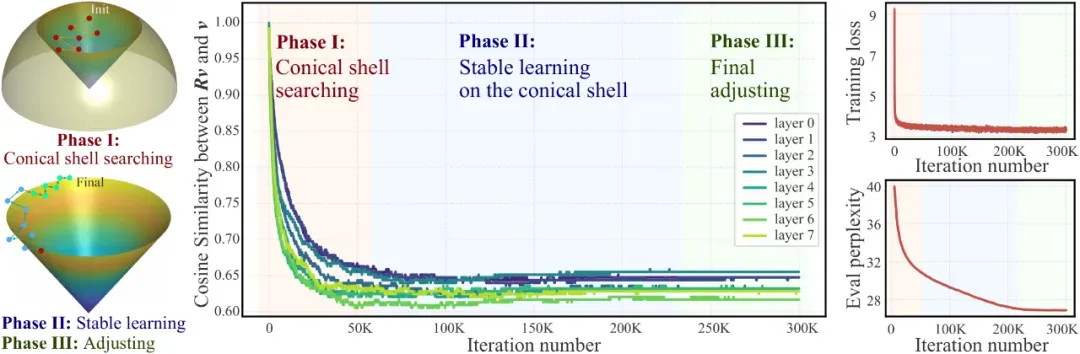
图 POET 的三个学习阶段:左—示意图;中—角度;右—损失值与验证。
谱性质与泛化
当前训练大型语言模型的事实标准是直接使用Adam优化器对权重矩阵进行更新。尽管这一做法实现简单,但在计算上往往代价高昂,随着模型规模的扩大,其复杂度迅速增长。此外,该方法对超参数极为敏感,需精细调整以保证训练稳定收敛。
更为关键的是,即便训练损失已经被有效最小化,模型的泛化性能仍可能表现不佳。为缓解这一问题,本文提出了多种权重正则化与归一化技术,其核心目标往往可归结为:显式或隐式地改善权重矩阵的谱结构(即奇异值分布)。
从直观角度看,权重矩阵的谱范数(最大奇异值)描述了其对输入向量的放大上界,因此与模型的平滑性和泛化能力密切相关。一般认为,较小的谱范数(意味着更温和的变换)往往有助于提升泛化性能。这一观点促使越来越多研究致力于对谱性质进行精细控制。理论研究亦表明,若能有效约束权重矩阵的谱结构,便可形式化地为模型提供泛化上的保证。
谱保持(Spectrum-preserving)权重更新
为在避免上述局限的同时实现有效的权重量谱控制,文章提出一种基于正交等价变换(OrthogonalEquivalenceTransformation)的重参数化训练算法,用于间接学习权重矩阵。具体而言,POET 将权重矩阵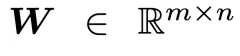 重参数化为
重参数化为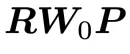 ,其中
,其中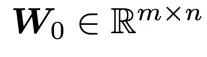 为随机初始化的权重矩阵,
为随机初始化的权重矩阵,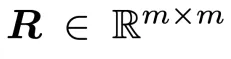 和
和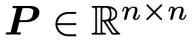 为两个可学习的正交矩阵。在训练过程中,POET 不直接优化权重矩阵,而是保持随机初始化矩阵
为两个可学习的正交矩阵。在训练过程中,POET 不直接优化权重矩阵,而是保持随机初始化矩阵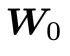 不变,通过学习正交矩阵
不变,通过学习正交矩阵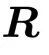 和
和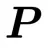 来变换
来变换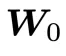 。这种重参数化策略在允许奇异向量灵活调整的同时,能够严格保持权重矩阵的奇异值谱,从而实现谱保持的权重更新。
。这种重参数化策略在允许奇异向量灵活调整的同时,能够严格保持权重矩阵的奇异值谱,从而实现谱保持的权重更新。
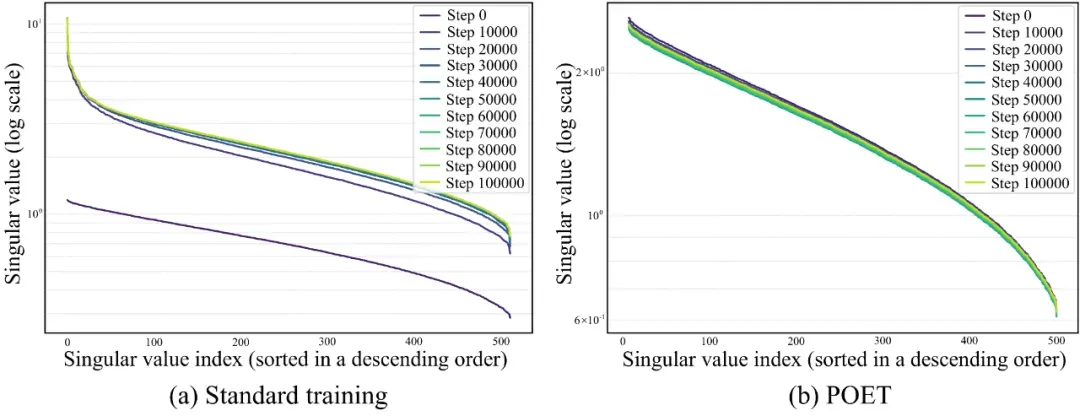
图 LLaMA模型中同一权重矩阵奇异值的训练动态。左图为标准训练,严格遵循大型语言模型的常规做法(使用AdamW直接优化);右图为POET,其采用本文提出的近似方法以支持大规模LLM训练。POET的奇异值仅出现轻微(几乎可忽略)的变化,主要归因于数值误差和近似误差。
奇异值谱的训练动态
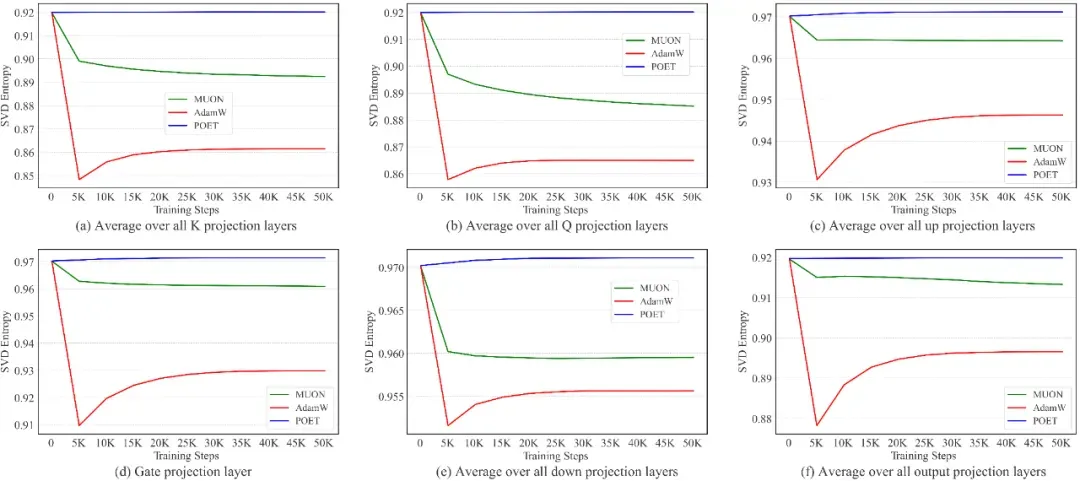
受 Muon [4]的启发,研究者对 AdamW、Muon与 POET 的奇异值谱进行了谱分析。在训练的不同迭代点,可对训练后的模型计算 SVD 熵
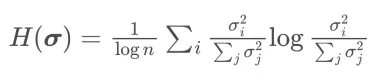
该指标用于衡量奇异值的多样性;熵值越高,表示谱分布越均匀、越丰富。[4] 将 Muon 相较于 AdamW 的优越性能归因于其权重矩阵更新所带来的更丰富谱分布。正如下图所示,由于采用正交等价变换,POET 在整个训练过程中始终保持较高的谱多样性。
POET方法具备两项核心优势:
- 高效的谱控制
由于正交变换并不改变权重矩阵的奇异值,POET在训练全程都能保持权重谱与随机初始化矩阵一致——即便采用近似实现,这一点也已得到实证验证。借助恰当的初始化方案,POET可直接约束奇异值分布,避免标准LLM训练后权重出现过大的奇异值。为进一步增强算法效果,研究者们提出了两种新初始化策略:归一化高斯初始化(normalizedGaussianinitialization)和 均匀谱初始化(uniformspectruminitialization),均可确保生成的权重矩阵具有有界奇异值。
- 高效近似
直接进行POET训练的计算开销较高,但方法本身的灵活性为高效、可扩展训练提供了空间。针对大规模正交矩阵优化这一关键难题,文章提出两级近似方案:
随机基元优化:将大正交矩阵分解为若干参数量更少的基元正交矩阵,并结合“合并再初始化”策略提高效率;
基于Cayley‑Neumann参数化的近似正交性:通过 Neumann 级数近似 Cayley 正交参数化,以较低计算成本保持正交性,同样借助“合并再初始化”策略抑制误差累积。
LLaMA架构的大规模语言模型预训练
本文在多种规模的LLaMATransformer(60M、130M、350M、1.3B 参数)上对POET进行了预训练实验。使用的数据集为C4——从CommonCrawl清洗得到的网页语料,已被广泛用于大型语言模型的预训练。下文汇总了实验结果,报告了验证困惑度(perplexity)及可训练参数量。
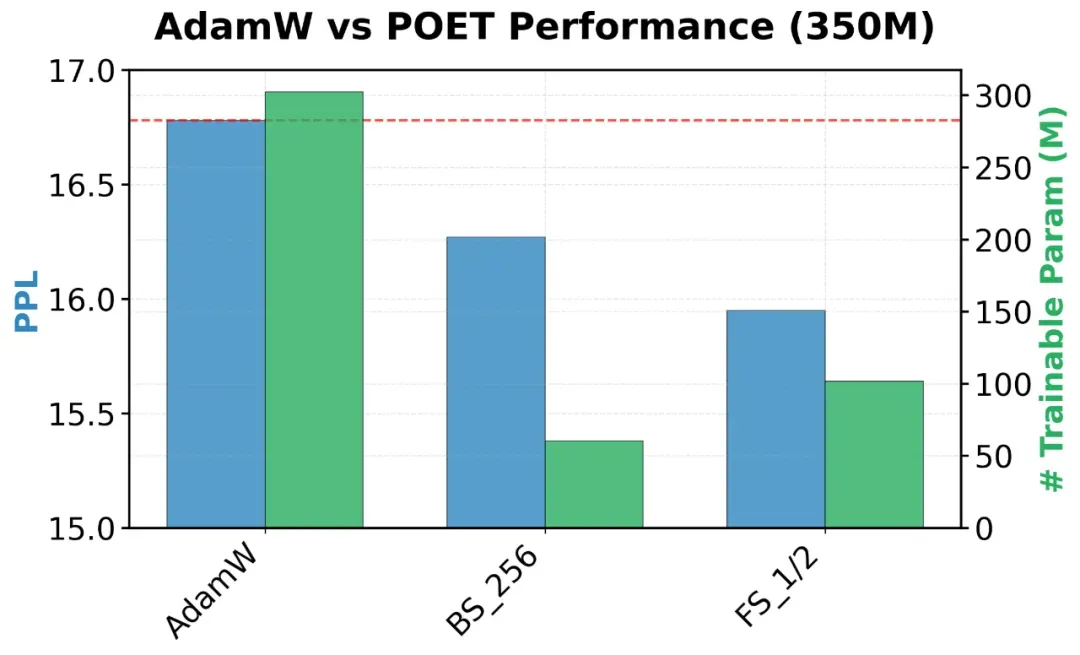
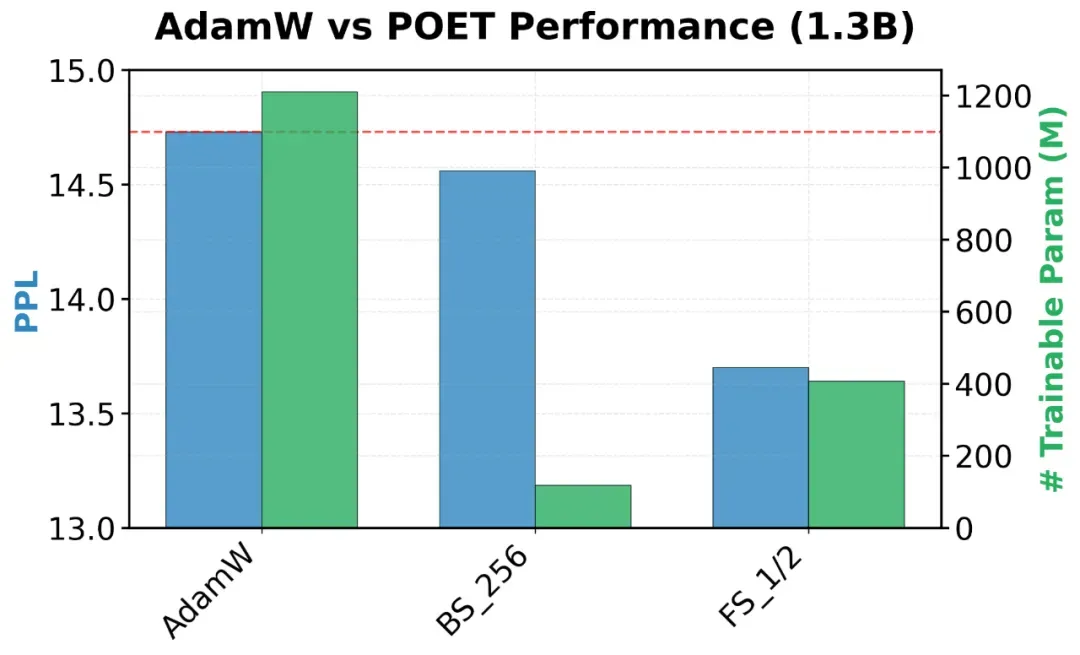
图 AdamW和POET在模型规模为350M和1.3B下的可训练参数规模及验证困惑度(perplexity)。
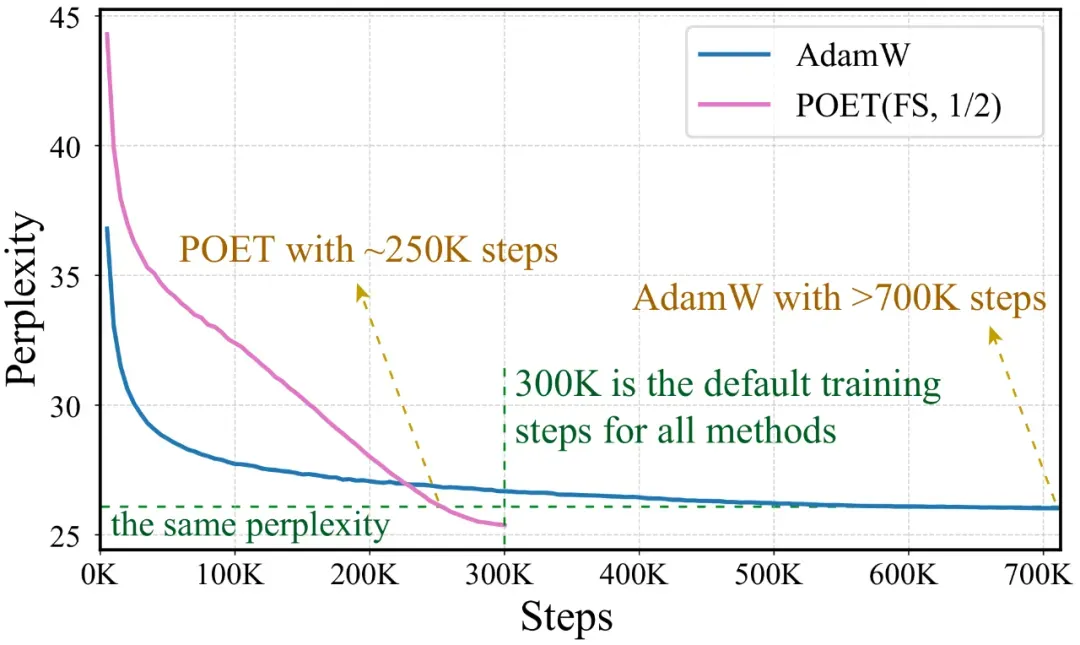
训练加速
为突出POET在性能上的显著改进,文章将AdamW的训练步数(即模型实际看到的token数量)大幅提升至原来的近三倍。即便如此,采用 b=1/2 设置的POET‑FS仍在性能上超越AdamW。
参数与内存复杂度
通过将超参数 b 作为采样预算引入,完全随机 SPO(StochasticPrimitiveOptimization)成功将参数复杂度与权重矩阵规模解耦。当 b 取较小值时,POET 的参数效率显著提升,但收敛速度有所下降,为使用者提供了效率与速度之间的灵活权衡。相比之下,块随机 SPO 的参数复杂度与矩阵尺寸(m+n)成正比,因而较 AdamW(需要 mn 个可训练参数)更具可扩展性。在内存占用方面,只要采样预算 b 设置得当,两种 POET 变体均可显著优于 AdamW。下文给出了参数与内存复杂度的详细对比。

训练算法
步骤1:权重初始化使用归一化高斯初始化为权重矩阵赋值: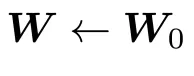
步骤2:正交矩阵初始化
完全随机SPO(fullystochasticSPO):随机采样索引集合 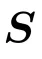 ,并使用CNP(Cayley‑NeumannParameterization)对
,并使用CNP(Cayley‑NeumannParameterization)对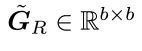 与
与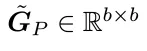 进行参数化。
进行参数化。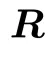 与
与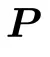 二者均以单位矩阵开始。
二者均以单位矩阵开始。
块随机SPO(block‑stochasticSPO):随机采样置换矩阵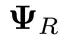 与
与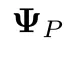 ,同样采用CNP对
,同样采用CNP对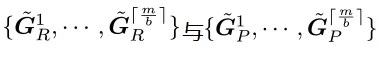 与进行参数化,并将它们初始化为单位矩阵。同样,
与进行参数化,并将它们初始化为单位矩阵。同样,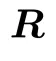 与
与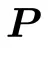 二者均以单位矩阵开始。
二者均以单位矩阵开始。
步骤3:高效正交参数化
对于完全随机SPO可得: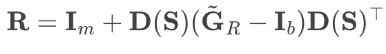 和
和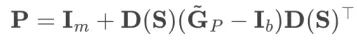 。
。
对于块随机SPO可得: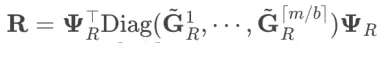 和
和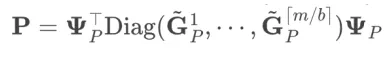 。
。
步骤4:正交矩阵内层训练循环更新
前向传播中的等效权重矩阵为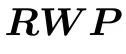 。
。
反向传播通过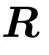 与
与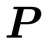 计算梯度,进而更新完全随机SPO中
计算梯度,进而更新完全随机SPO中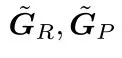 的或块随机SPO中的
的或块随机SPO中的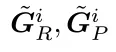 ;该内循环迭代次数固定。
;该内循环迭代次数固定。
步骤5:合并并重新初始化(merge‑then‑reinitialize)
将已学习的正交矩阵合并进权重: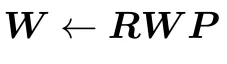 。
。
若训练未结束,则返回步骤2,重新初始化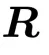 与
与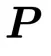 ,继续下一阶段训练。
,继续下一阶段训练。
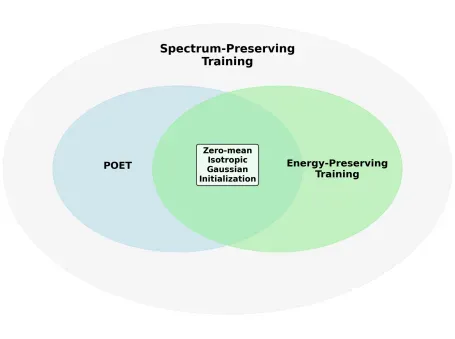
POET的优异表现来自于超球能量与谱保持
神经元初始化
鉴于 POET 在训练过程中会保留初始权重矩阵的谱特性,初始化策略显得至关重要。文章运用了归一化高斯初始化:先从零均值、固定方差的高斯分布中抽取神经元权重,再对其进行归一化。下表对多种随机初始化方案进行了实证比较,结果显示归一化高斯初始化取得了最佳最终性能。研究者推测,这一优异表现源于 POET 在该初始化下能够在训练过程中同时保持超球能量与谱特性。

训练中的超球能量
超球能量 HE 用于衡量神经元在单位超球面上的均匀分布程度,可作为刻画各层神经表征的一种度量。文献[2,3]表明,满足正交约束的训练过程可在训练期间保持这一超球能量不变,从而避免表征退化并提升泛化性能。
归一化高斯初始化下的POET 可同时保持能量与奇异值分布
在零均值、各向同性的高斯初始化条件下,POET 能够同时实现谱保持训练与能量保持训练。这一特性为归一化高斯初始化方法的最优性能提供了理论解释(详细证明参见附录 B)。
POET训练机理解析
为深入理解POET的运行机制,我们用向量探测(vector probing)分析正交矩阵的学习动态。具体做法是:固定随机生成的单位向量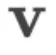 ,计算
,计算 ,即
,即 与
与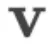 之间的余弦相似度,以评估正交矩阵
之间的余弦相似度,以评估正交矩阵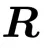 和
和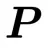 的演化。
的演化。
对七个可学习的正交矩阵在训练过程中的余弦相似度进行跟踪后,可以将其学习过程划分为三个阶段(见图1):
- 锥壳搜索阶段(Conical shell searching)
余弦相似度从1(即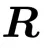 为单位矩阵)逐渐下降并收敛到[0.60,0.65]。这一现象在所有正交矩阵上均一致,说明
为单位矩阵)逐渐下降并收敛到[0.60,0.65]。这一现象在所有正交矩阵上均一致,说明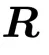 将
将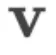 映射到其原始方向附近的狭窄锥壳上。
映射到其原始方向附近的狭窄锥壳上。
- 锥壳上的稳定学习阶段(Stable learning on the conical shell)
余弦相似度保持在该区间内不再显著变化,但模型开始进入稳定学习期;尽管余弦值趋于稳定,验证困惑度仍在线性下降。
- 最终阶段微调(Final adjusting)
随着学习率逐步衰减至零,学习速度放缓并最终停止。
更为详尽的讨论与实证结果见论文附录。



