2017 年，一篇《Attention Is All You Need》论文成为 AI 发展的一个重要分水岭，其中提出的 Transformer 依然是现今主流语言模型的基础范式。尤其是在基于 Transformer 的语言模型的 Scaling Law 得到实验验证后，AI 领域的发展更是进入了快车道。
现如今，这篇论文的引用量正向 19 万冲刺，而 Transformer 和注意力机制本身也已经历了很多改进和创新，比如我们前段时间报道过的「Multi-Token Attention」和「Multi-matrix Factorization Attention」等。
随着 AI 的不断发展，现如今的一个重要挑战是如何获得足够多高质量的 token。又或者，该如何更高效地利用这些 token？为此，还必须对 Transformer 进行进一步的升级改造。
近日，Meta 的一篇论文公布了他们在这方面取得的一个新进展，提出了一种旋转不变型三线性注意力机制，并证明其表示能力与 2-simplicial Transformer 相当。更重要的是，它的表现甚至足以改变 Scaling Law 中的系数。Meta 也用 Triton 实现了这种注意力机制。
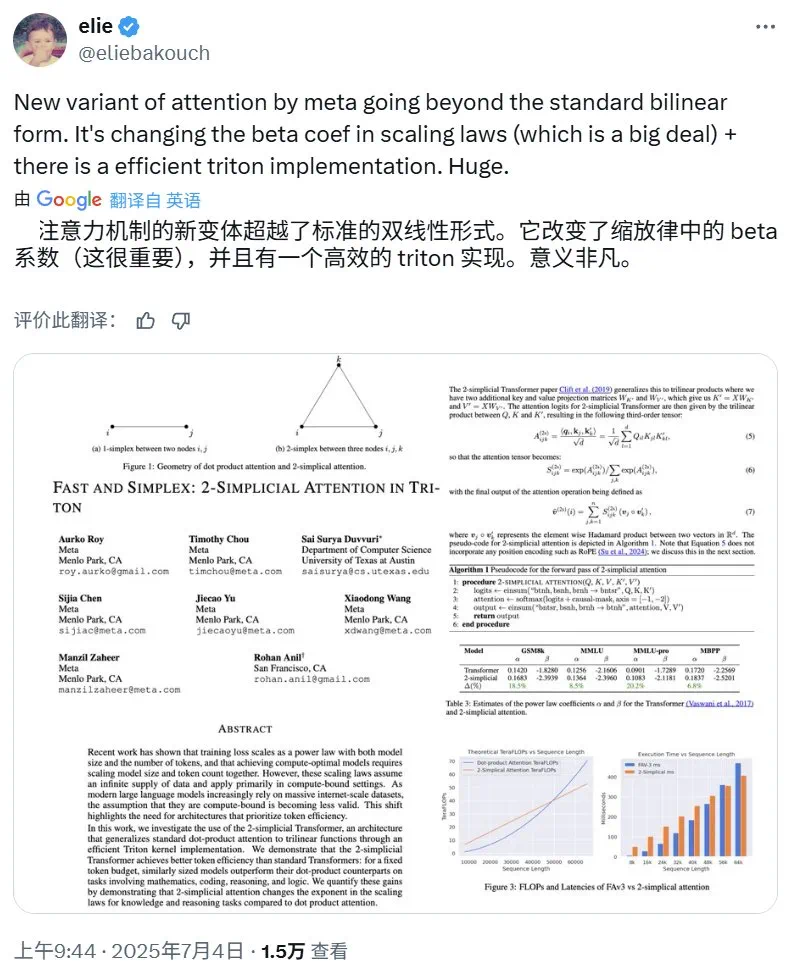
该研究基于 RoPE 向三线性函数的泛化；而 2-simplicial Transformer 则源自 2019 年 Clift et al. 的研究《Logic and the 2-Simplicial Transformer》，其中将 Transformer 的点积注意力机制泛化到了三线性形式。
论文标题：Fast and Simplex: 2-Simplicial Attention in Triton
论文地址：https://arxiv.org/pdf/2507.02754.pdf
他们进一步证明，在有限的 token 预算下，2-simplicial Transformer 的扩展性优于 Transformer。
此外，他们的实验还表明，2-simplicial Transformer 相对于 Transformer 具有更有利的参数数量 scaling 指数。这表明，与 Chinchilla scaling 不同，有可能以比 2-simplicial Transformer 的参数增长更慢的速度增加 token 数量。
研究结果表明，在 token 约束下运行时，与点积注意力机制 Transformer 相比，2-simplicial Transformer 可以更有效地逼近自然语言的不可约熵。
神经 Scaling Law 概述
要理解这项研究的意义，首先需要了解一下 Scaling Law。
简单来说，就是损失 L 会随模型参数总数 N 和 token 数量 D 呈幂律衰减：
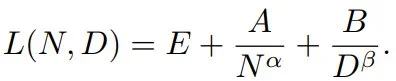
其中，第一项 E 通常被描述为不可约损失，对应于自然文本的熵。第二项描述了这样一个事实：具有 N 个参数的模型的表现达不到理想的生成过程。第三项则对应于这样一个事实：我们仅使用有限的数据样本进行训练，并且没有将模型训练到收敛。
理论上，当 N → ∞ 且 D → ∞ 时，大型语言模型应该接近底层文本分布的不可约损失 E。
对于给定的计算预算 C，其中 F LOP s (N, D) = C，可以将最佳参数数量表示为 Nopt ∝ C a，将最佳数据集大小表示为 Dopt ∝ C b。Hoffmann 等人 (2022) 的作者进行了多项实验，并将参数函数拟合到损失函数中，以估计指数 a 和 b：多种不同的方法证实，a 大约为 0.49，b 大约为 0.5。这引出了 Hoffmann 等人 (2022) 的核心论点：必须根据模型大小按比例缩放 token 数量。
对于给定的计算预算 C，其中 FLOPs (N, D) = C，可以将最佳参数数量表示为 N_opt ∝ C^a，将最佳数据集大小表示为 D_opt ∝ C^b。Hoffmann et al. (2022) 进行了多次实验，并根据损失拟合了参数函数，以估计指数 a 和 b。
结果，通过多种不同方法发现：a 约为 0.49，b 约为 0.5。
如此，便引出了 Hoffmann et al. (2022) 的一个核心论点：必须根据模型大小按比例扩展 token 数量。
但是，正如前面讨论的那样，足够高质量且足够数量的 token 是预训练扩展的新瓶颈，因此需要探索替代的训练算法和架构。另一方面，最近的研究表明，之前文献中提出的大多数建模和优化技术仅仅改变了误差（偏移了 E），并没有从根本上改变幂律中的指数。谷歌 DeepMind 的研究者 Katie Everett 对此进行过精彩的讨论：
https://x.com/_katieeverett/status/1925665335727808651
2-simplicial Transformer
2-simplicial Transformer 由 Clift et al. (2019) 提出，他们将点积注意力机制从双线性扩展为三线性形式，也就是从 1-simplex 扩展成了 2-simplex。
先来看看标准的注意力机制：
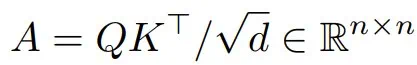
其中，每一项都是点积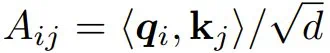 
。
然后，通过逐行 softmax 运算将注意力分数（logit）转换为概率权重：
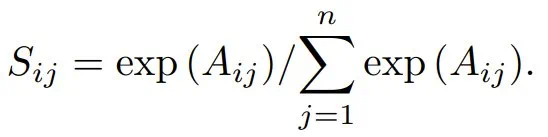
注意力层的最终输出是根据这些注意力分数对这些值进行线性组合得到的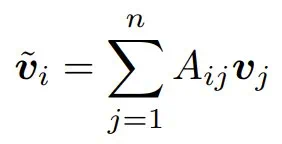
。
Clift et al. (2019) 的 2-simplicial Transformer 论文将其推广到三线性积，其中有两个额外的键和值投射矩阵 W_K′ 和 W_V′，从而得到 K′ = XW_K′ 和 V′ = XW_V′。然后，2-simplicial Transformer 的注意力 logit 由 Q、K 和 K′ 的三线性积给出，从而得到以下三阶张量：
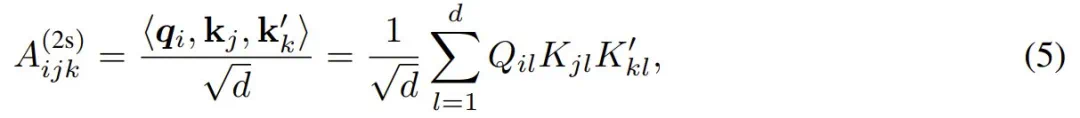
从而注意力张量变为：
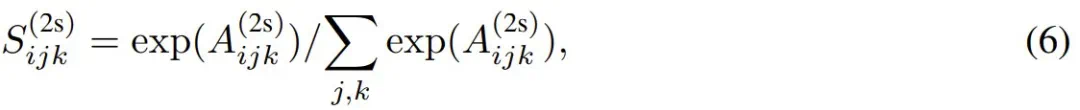
注意力运算的最终输出定义为：
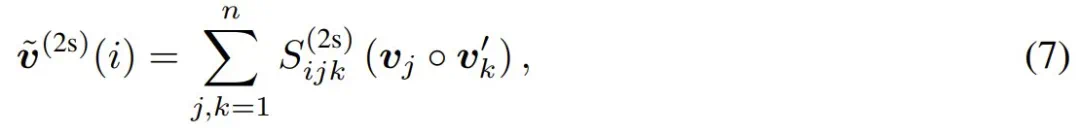
其中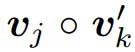 
表示两个向量的元素级 Hadamard 积。2-simplicial Transformer 的伪代码如算法 1 所示。注意，公式 5 不包含 RoPE 等任何位置编码。
基于行列式的三线性形式
Su et al., 2024 提出 RoPE 时，是想将其作为一种用于 Transformer 语言模型的序列位置信息捕获方法。RoPE 对查询 q_i 和键 k_j 应用位置相关的旋转，使得点积 <q_i, K_j> 是相对距离 i-j 的函数。特别需要注意的是，点积对于正交变换 R 具有不变性：
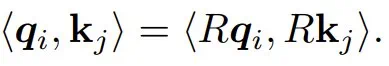
这对于 RoPE 至关重要，因为对于同一位置 i 相同的查询 q_i 和键 k_i，我们期望其点积不会因基于位置的旋转而发生变化。请注意，(5) 式中定义的三线性形式并非是旋转不变，并且对 q_i 、k_i 和 k′_i 进行相同的旋转不再保留内积。因此，为了将 RoPE 泛化到 2-simplicial 注意力模型，探索其他具有旋转不变性的双线性和三线性形式至关重要。
而 Meta 的这个团队注意到，以下函数也具有旋转不变性：
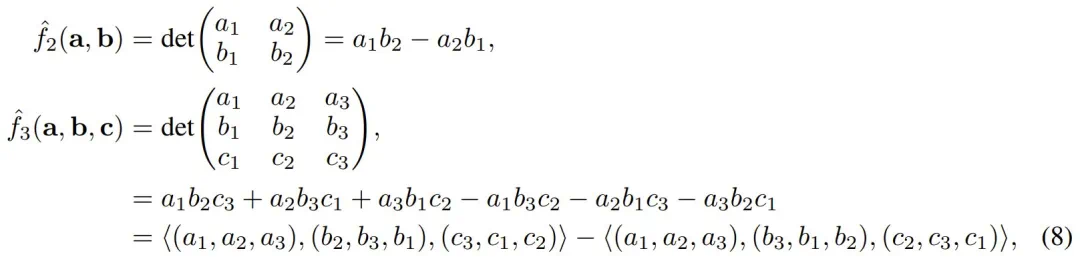
可以使用带符号的行列式运算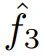 
来计算 A^(det) ∈ ℝ^n×n×n。对于任意向量 q，令 q^(l) = q = q [3 (l - 1) : 3l] 为其第 l 个大小为 3 的块。其 logit 定义为：
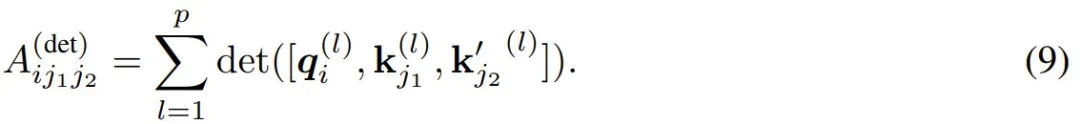
由于公式 8 根据 Sarrus 规则包含 2 个点积项，因此需要修改算法 1，使用 2 个 einsum 而不是第 2 行中的 1 个。最终的注意力权重 S 是通过对上述 logit 应用 softmax 函数来计算的，类似于公式 6。然后，token i 的输出是值向量的加权和，如公式 7 所示。
定理：对于任意输入大小 n 和输入范围 m = n^{O (1)}，存在一个具有单个注意力头的 Transformer 架构，其 logit 计算方式如公式 (9) 所示，注意力头维度为 d = 7，使得对于所有 X ∈ [M]^N，如果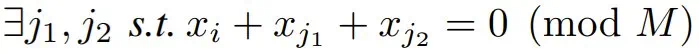
，则 Transformer 对元素 x_i 的输出为 1，否则为 0。
对该定理的证明请见原论文附录。
模型设计
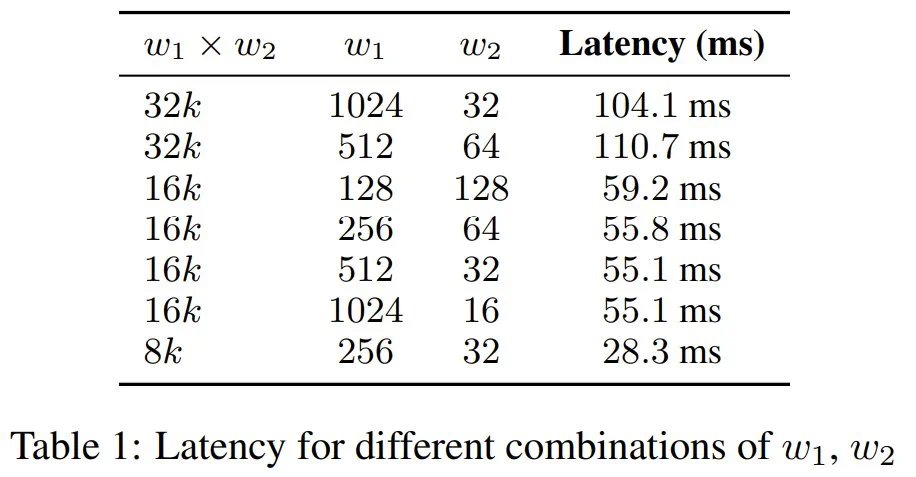
由于 2-simplicial 注意力在序列长度 n 上的扩展复杂度为 O (n^3)，因此将其应用于整个序列是不切实际的。该团队的做法是将其参数化为 O (n× w_1 × w_2)，其中 w_1 和 w_2 定义的是序列上滑动窗口的维度。每个查询向量 Q_i 会关注 w_1 个 K 键和 w_2 个 K′ 键的局部区域，从而减轻计算负担。该团队系统地评估了 w_1 和 w_2 的各种配置，以确定计算效率和模型性能之间的最佳平衡点（见表 1）。
对于因果点积注意力机制，长度为 n 的序列的复杂度由下式给出：
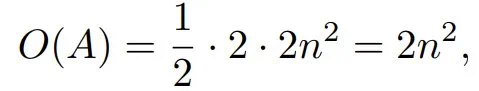
其中 n 是序列长度。这涉及两次矩阵乘法：一次用于 Q@K，一次用于 P@V，每次乘法每个元素都需要两次浮点运算。因果掩码使其能够跳过 1/2 的计算。
相比之下，以 w_1 和 w_2 为参数的 2-simplicial 注意力机制的复杂度表示为：
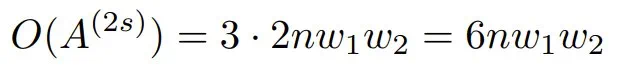
其复杂度的增长来源是三线性 einsum 运算，与标准点积注意力机制相比，它需要进行一次额外的乘法运算。
该团队选择窗口大小为 (512, 32)，以平衡延迟和质量。在此配置下，2-simplicial 注意力机制的计算复杂度与 48k 上下文长度的点积注意力机制相当。
图 2 给出了一个实现。因此，像在 Flash 注意力机制中那样平铺式查询 Q 会导致计算吞吐量较低。受 Native Sparse Attention 的启发，Meta 该团队采用的模型架构利用了较高 (64) 的分组查询注意力 (GQA) 比率。这种方法能够沿着查询头高效地平铺，确保密集计算，并消除昂贵的逐元素掩码。
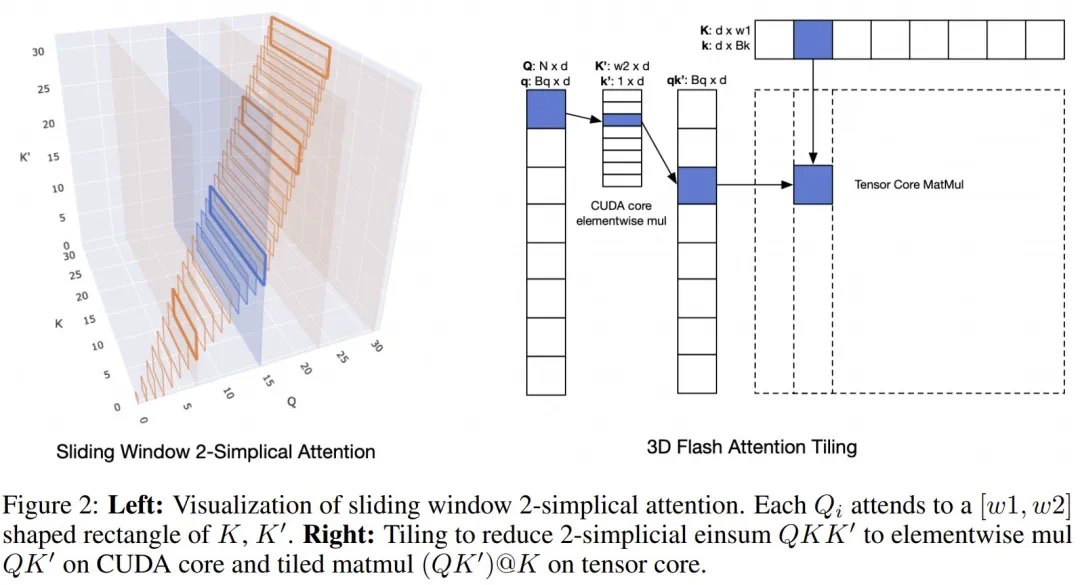
该团队还引入了一系列针对 2-simplicial 注意力的核优化，这些优化基于使用在线 softmax 的 Flash Attention。详见原论文。下面来重点看看实验表现。
实验与结果
这个团队训练了一系列 MoE 模型，其参数范围从 1B 活动参数和 57B 总参数到 3.5B 活动参数和 176B 总参数。具体配置见原论文。
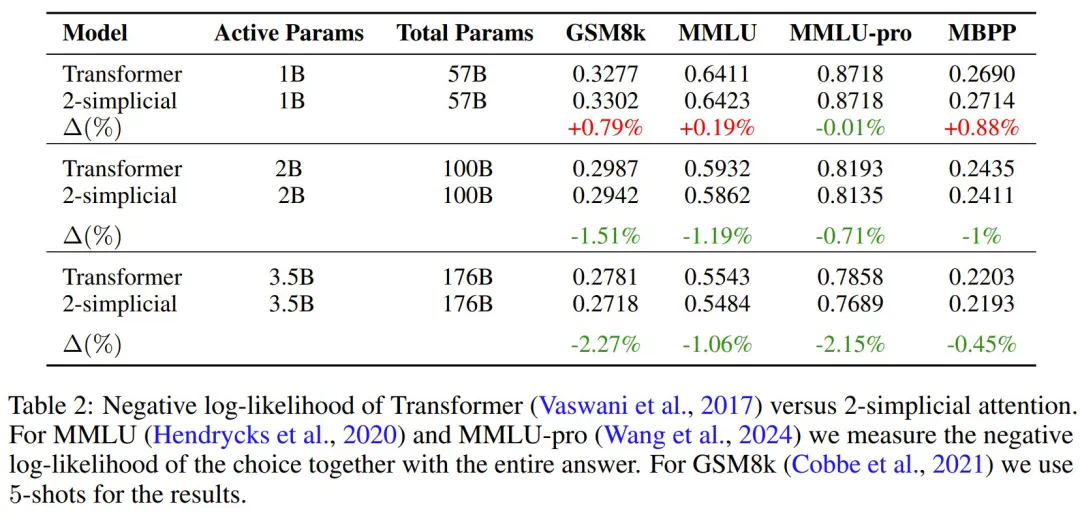
该团队发现，从 1B （活动）参数模型到 3.5B （活动）参数模型，负对数似然的扩展（∆）出现了下降。
此外，在小于 2B （活动）参数的模型中，使用 2-simplicial 注意力机制没有任何好处。
基于此，该团队估算了 2-simplicial 注意力机制与点积注意力机制的幂律系数有何不同。基于前述方法，其损失可以表示为：
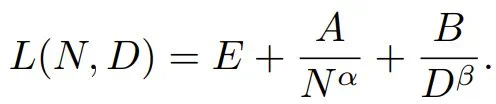
由于训练这两个模型使用的 token 数量相同，因此可以忽略第三项，将损失简化为：
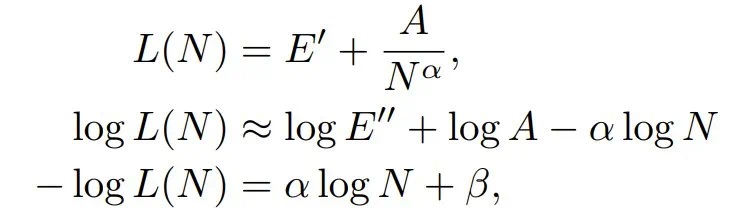
其中 β = - log E′′ - logA ，由于 E′ 较小，E′′ 是 E′ 的近似值。注意，这里使用了 log (a + b) = log (1 + a/b) + log (b) 来分离这两个项，并将 1 + a/b 项隐藏在 E′′ 中。
因此，可以根据表 2 中的损失估算两组模型的 α 和 β，其中 N 代表每个模型中的有效参数。
该团队在表 3 中估计了 Transformer 和 2-simplicial Transformer 的斜率 α 和截距 β。
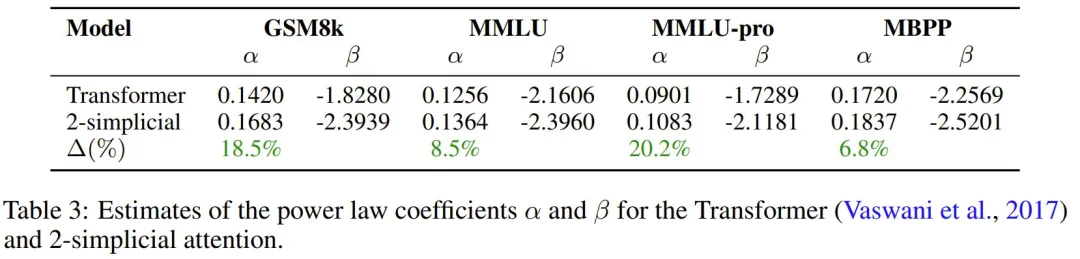
可以看到，与点积注意力 Transformer 相比，2-simplicial 注意力具有更陡的斜率 α，即其 Scaling Law 的指数更高。
