Poseidon

偏微分方程有了基础模型：样本需求数量级减少，14项任务表现最佳

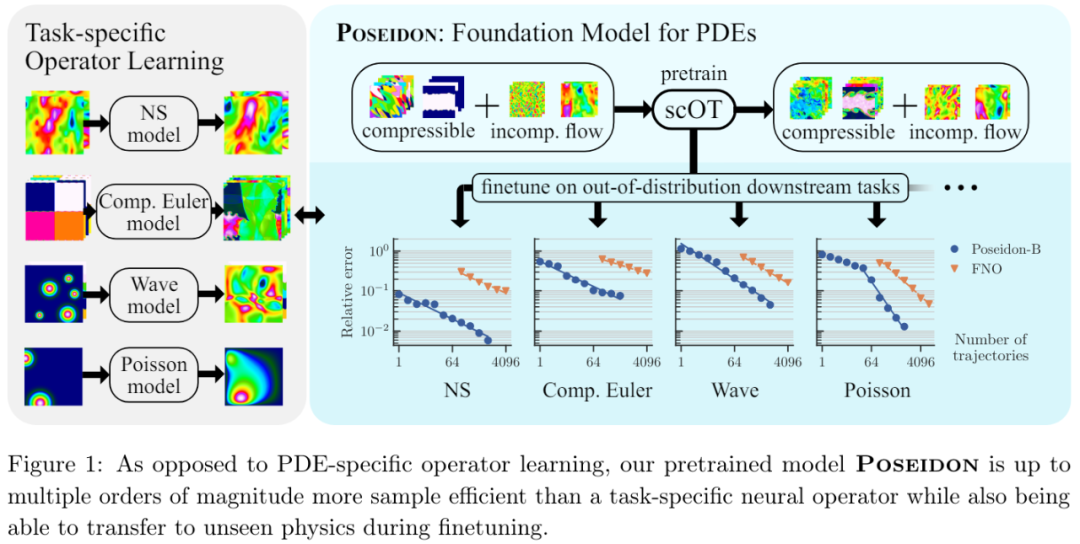
本文提出的 Poseidon 在样本效率和准确率方面都表现出色。偏微分方程（PDEs）被称为物理学的语言，因为它们可以在广泛的时间 - 空间尺度上对各种各样的物理现象进行数学建模。常用的有限差分、有限元等数值方法通常用于近似或模拟偏微分方程。然而，这些方法计算成本高昂，特别是对于多查询问题更是如此，因而人们设计了各种数据驱动的机器学习（ML）方法来模拟偏微分方程。其中，算子学习（ operator learning）算法近年来受到越来越多的关注。然而，现有的算子学习方法样本效率并不高，因为它们需要大量的训练样例才能

6/11/2024 12:52:00 AM

机器之心

资讯热榜

上海AI实验室开源InternVL3系列多模态大型语言模型 Haisnap横空出世，小白用户也能轻松打造AI应用「交交」媲美GPT-4o！上海交大推出口语对话情感大模型，首个纯学术界自研！ OpenAI开源超Agent:Codex CLI,五小时内破 5000 颗星 ChatGPT重磅更新：新增图像库功能，可查看自己用GPT生成的所有图片本地部署DeepSeek+DiFy平台构建智能体应用 kimi开源视觉语言模型 Kimi-VL 与 Kimi-VL-Thinking，多项基准超越 GPT-4o OpenAI 发布“智能体构建实战指南”实用性文档（附文档资源）

标签云

人工智能 OpenAI AIGC AI ChatGPT DeepSeek AI绘画数据机器人谷歌模型大模型 Midjourney 智能用户学习开源 GPT 微软 Meta AI创作图像技术论文 Stable Diffusion 马斯克 Gemini 算法蛋白质生成式芯片代码英伟达腾讯神经网络计算研究 Sora AI for Science 3D Anthropic AI设计机器学习 GPU 开发者场景华为预测伟达 Transformer 百度人形机器人苹果深度学习 AI视频模态字节跳动 xAI 驾驶文本搜索大语言模型 Claude Copilot 具身智能神器推荐 LLaMA 算力安全应用视频生成科技视觉亚马逊干货合集 2024 AGI 特斯拉大型语言模型训练