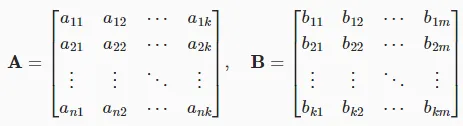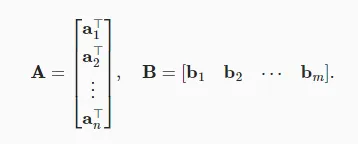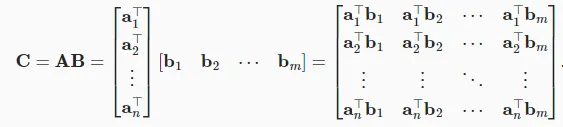一文详解深度学习中的标量、向量、矩阵、张量

在深度学习领域，标量、向量、矩阵和张量是不可或缺的基本概念。它们不仅是数学工具，更是理解和构建神经网络的关键。从简单的标量运算到复杂的张量处理，这些概念贯穿于数据表示、模型构建和算法优化的全过程。本文将简要介绍这些数学基础，帮助读者更好地理解它们在深度学习中的作用和应用。

1、标量

定义：仅包含一个数值的量，像北京温度 52°F，其中 52 就是标量。在数学里，标量变量常用普通小写字母（如 x、y、z）表示 ，所有（连续）实数标量的空间用 R 表示，x ∈ R 表示 x 是实值标量。

表示与运算：由只有一个元素的张量表示。通过代码能对其进行加、乘、除、指数等算术运算。

示例：

import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)
x + y, x * y, x / y, x**y

结果：

2、向量

定义：可看作标量值组成的列表，其元素或分量具有实际意义。在数学表示法中，向量通常记为粗体、小写符号（如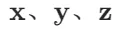），通过一维张量表示。

表示与运算：用下标引用元素，如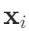。向量默认方向是列向量。

示例：

x = torch.arange(4)
x

结果：

向量长度通常称为向量的维度，与普通的Python数组一样，可以通过调用Python的内置len()函数来访问张量的长度。

当用张量表示一个向量（只有一个轴）时，也可以通过.shape属性访问向量的长度。 形状（shape）是一个元素组，列出了张量沿每个轴的长度（维数）。 对于只有一个轴的张量，形状只有一个元素。

x.shape
# 结果：torch.Size([4])

注意，维度（dimension）这个词在不同上下文时往往会有不同的含义，这经常会使人感到困惑。 为了清楚起见，明确：向量或轴的维度被用来表示向量或轴的长度，即向量或轴的元素数量。 然而，张量的维度用来表示张量具有的轴数。 在这个意义上，张量的某个轴的维数就是这个轴的长度。

3、矩阵

定义：是向量从一阶到二阶的推广，通常用粗体、大写字母（如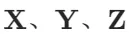

表示：矩阵元素用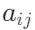表示，可通过行、列索引访问。

当调用函数来实例化张量时， 可以通过指定两个分量m和n来创建一个形状为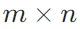的矩阵。

A = torch.arange(20).reshape(5, 4)
A

结果：

交换矩阵的行和列时，结果称为矩阵的转置（transpose）。 通常用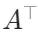来表示矩阵的转置：

A.T

结果：

4、张量

定义：就像向量是标量的推广，矩阵是向量的推广一样，张量是描述具有任意数量轴的n维数组的通用方法，可以构建具有更多轴的数据结构。 例如，向量是一阶张量，矩阵是二阶张量。

表示与运算：尤其在处理图像等数据时，张量变得更加重要。一般来说，图像以n维数组形式出现， 其中3个轴对应于高度、宽度，以及一个通道（channel）轴， 用于表示颜色通道（红色、绿色和蓝色）。

X = torch.arange(24).reshape(2, 3, 4)
X

结果：

5、张量算法的基本性质

张量算法的基本性质在深度学习中至关重要，它包括按元素运算的形状不变性、张量间运算结果的形状规律、与标量运算的特点，以及降维、非降维求和与累积求和等操作特性。这些性质贯穿于深度学习的各类计算中，对理解和运用深度学习模型起着关键作用，具体如下：

按元素运算的形状不变性

从按元素操作的定义可知，任何按元素的一元运算都不会改变其操作数的形状。例如，对一个张量进行取绝对值、平方等一元运算，运算后的张量形状与原张量保持一致。这一性质确保了在对张量的每个元素进行单独操作时，数据的结构不会被破坏，为后续基于张量形状的计算和处理提供了稳定性。

张量间运算结果的形状规律

给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量。

两个相同形状的矩阵相加，会在这两个矩阵上执行元素加法，得到的结果矩阵形状与原矩阵相同。这一性质使得在进行张量间的批量运算时，无需担心形状不匹配的问题，提高了计算的效率和准确性。

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A + B

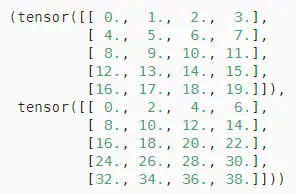
与标量运算的特点

将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。这种特性在深度学习中常用于对张量进行缩放或平移操作，以调整数据的分布或特征的强度。

a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape

降维操作

求和降维：可以对任意张量进行元素求和操作，默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
A.sum()
# 结果：tensor(190.))

也可指定张量沿某一个轴来通过求和降低维度， 以矩阵为例，为了通过求和所有行的元素来降维（轴0），可以在调用函数时指定axis=0。

A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
# 结果：(tensor([40., 45., 50., 55.]), torch.Size([4]))

指定axis=1将通过汇总所有列的元素降维（轴1）

A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
# 结果：(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))

对于一个三维张量，轴（axis）的定义如下：

轴0（axis=0）：通常表示张量中的第一个维度，可以理解为不同的数据样本或者批次（batch）。

轴1（axis=1）：通常表示张量中的第二个维度，可以理解为数据的行。

轴2（axis=2）：通常表示张量中的第三个维度，可以理解为数据的列。

平均值计算：平均值是与求和相关的量，通过将总和除以元素总数来计算。计算平均值的函数也可沿指定轴降低张量的维度。如A.mean(axis = 0)计算矩阵 A 按列的平均值，A.mean()计算所有元素的平均值。

A.mean(), A.sum() / A.numel() # 结果：(tensor(9.5000), tensor(9.5000))
A.mean(axis=0), A.sum(axis=0) / A.shape[0] # 结果：(tensor([ 8.,  9., 10., 11.]), tensor([ 8.,  9., 10., 11.]))

非降维求和与累积求和

非降维求和：有时在调用函数计算总和或均值时保持轴数不变很有用。

例如sum_A = A.sum(axis = 1, keepdims = True)，对矩阵 A 按行求和后仍保持两个轴，结果形状为 (5, 1) 。

sum_A = A.sum(axis=1, keepdims=True)
sum_A

由于 sum_A 在对每行进行求和后仍保持两个轴，这样可以通过广播将 A 除以 sum_A，实现按行的归一化等操作。

A / sum_A

沿某个轴计算 A 元素的累积总和， 比如 axis=0 （按行计算），可以调用 cumsum 函数。 此函数不会沿任何轴降低输入张量的维度。

累积求和：沿某个轴计算张量元素的累积总和，如A.cumsum(axis = 0)按行计算累积总和，此函数不会沿任何轴降低输入张量的维度。在分析时间序列数据或逐步累加的特征时，累积求和操作能帮助获取数据的累积趋势和状态。

A.cumsum(axis=0)

点积（Dot Product）

给定两个向量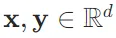， 它们的点积（dot product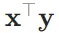）（或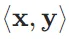） 是相同位置的按元素乘积的和：。

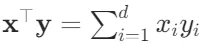1.torch.dot

功能：torch.dot用于计算两个一维向量的点积（Dot Product）。
 输入要求：两个输入必须是一维向量（即形状为(n,)的张量），且长度相同。
 输出：返回一个标量，表示两个向量的点积。
 
 
 
 
 
 import torcha = torch.tensor([1, 2, 3])b = torch.tensor([4, 5, 6])dot_product = torch.dot(a, b)print("点积结果：", dot_product)  # 输出：32

torch.dot用于计算两个一维向量的点积（Dot Product）。
import torch
a = torch.tensor([1, 2, 3])
b = torch.tensor([4, 5, 6])
dot_product = torch.dot(a, b)
print("点积结果：", dot_product)  # 输出：32

2.torch.matmul

• 功能：torch.matmul用于计算两个张量的矩阵乘积（Matrix Product），支持一维向量、二维矩阵以及更高维度张量的乘法。
• 输入要求：对于一维向量，torch.matmul会将它们视为行向量和列向量，计算它们的矩阵乘积。对于二维矩阵，torch.matmul计算矩阵乘法。对于高维度张量，torch.matmul会计算批量矩阵乘积。
• 输出：返回一个张量，形状根据输入张量的形状决定。

import torch
# 一维向量
a = torch.tensor([1, 2, 3])
b = torch.tensor([4, 5, 6])
# torch.matmul 会将一维向量视为行向量和列向量，计算矩阵乘积
matmul_result = torch.matmul(a, b)
print("矩阵乘积结果：", matmul_result)  # 输出：32
# 二维矩阵
A = torch.tensor([[1, 2], [3, 4]])
B = torch.tensor([[5, 6], [7, 8]])
matrix_product = torch.matmul(A, B)
print("矩阵乘积结果：\n", matrix_product)
# 输出：
# tensor([[19, 22],
#         [43, 50]])

对于一维向量
torch.dot(a, b)
torch.matmul(a, b)
torch.dot
torch.matmul
(1,)

对于二维及高维矩阵：torch.matmul可以计算矩阵乘积，但torch.dot不能用于二维矩阵。

Hadamard积

两个矩阵的按元素乘法称为Hadamard积（Hadamard product）（数学符号

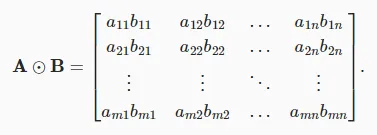
A * B

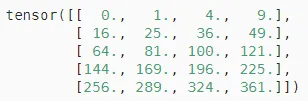
在深度学习中，Hadamard 积和点积的应用场景

Hadamard 积是指两个相同维度的张量逐元素相乘，通常用于以下场景：

1. 激活函数的逐元素操作：在神经网络中，激活函数（如 ReLU、Sigmoid 或 Tanh）通常对输入张量逐元素应用。这种操作可以看作是输入张量与一个逐元素的非线性函数的 Hadamard 积。例如，output = activation(input)，其中activation是逐元素的非线性函数。
2. 特征融合：在多特征融合时，Hadamard 积可以用于将不同来源的特征逐元素相乘，从而实现特征的加权融合。例如，在某些注意力机制中，通过 Hadamard 积对特征进行加权，以突出重要特征。
3. LSTM 门控机制：在长短期记忆网络（LSTM）中，Hadamard 积用于计算遗忘门和输入门的输出。遗忘门和输入门的输出通过 Hadamard 积逐元素作用于细胞状态。具体公式为：。
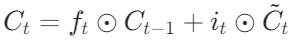4. 图像处理：在图像处理中，Hadamard 积可以用于图像融合。例如，将不同波段的图像逐元素相乘，以增强特定的光谱特征。此外，Hadamard 积还可以用于图像滤波，通过逐元素相乘实现特定的滤波效果。

点积通常用于计算两个向量的相似度或进行线性变换，常见于以下场景：

1. 注意力机制：点积在注意力机制中广泛使用，用于计算查询（query）和键（key）之间的相似度。例如，在点积注意力机制中，通过计算查询和键的点积来生成注意力权重。具体公式为：。
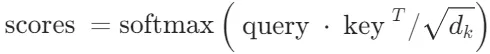2. 卷积神经网络（CNN）：在卷积层中，卷积核与输入特征图的卷积操作本质上是点积计算。每个神经元与输入特征图上的一个小区域进行点积运算，从而提取出有用的特征。
3. 特征向量的相似度计算：在自然语言处理（NLP）中，词向量之间的点积可以用于计算词与词之间的相似度。例如，通过点积计算两个词向量的相似度，进而实现文本分类和情感分析。
4. 正则化：在 L2 正则化（权重衰减）中，点积用于计算权重矩阵的 Frobenius 范数。具体来说，权重矩阵与自身的点积（即 Frobenius 内积）用于正则化项。

总结：

• Hadamard 积：适用于逐元素操作，如激活函数、特征融合、LSTM 门控机制和图像处理。
• 点积：适用于计算向量相似度、卷积操作、注意力机制和正则化。

矩阵-向量积

定义：设矩阵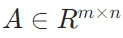，向量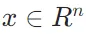，那么矩阵 - 向量积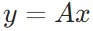是一个m维向量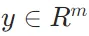。其计算方式是y的第i个元素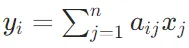，其中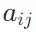是矩阵A的第i行第j列的元素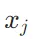，是向量x的第j个元素。

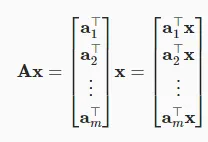
几何意义：矩阵 - 向量积可以看作是对向量x进行线性变换，将其从n维空间映射到m维空间。例如，在二维平面中，一个2×2的矩阵可以对平面上的向量进行旋转、缩放等操作。

计算示例：

• 设矩阵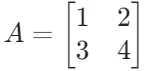，向量。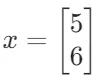
• 则。

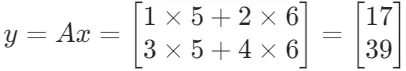torch.mv(A, x)

矩阵-矩阵乘法

定义：设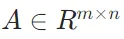矩阵，矩阵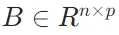，则矩阵C=AB是一个m×p的矩阵，其中C的第i行第j列的元素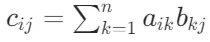。这意味着C的每个元素是A的对应行与B的对应列的元素乘积之和。

几何意义：矩阵 - 矩阵乘法可以表示多个线性变换的复合。例如，先进行一个旋转变换，再进行一个缩放变换，这两个变换对应的矩阵相乘就得到了表示这两个变换复合效果的矩阵。

计算示例：

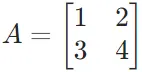• 设矩阵，矩阵。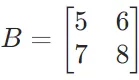
• 则。

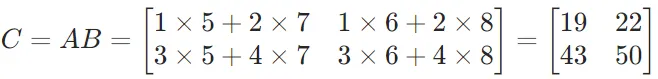torch.mm(A, B)