 图片
图片
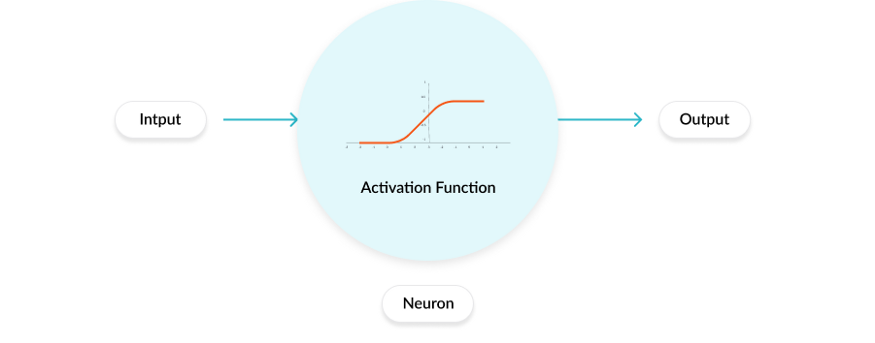
快速提示:只需记住,隐藏层和输出层对激活函数类型的要求通常不同,因此通常会使用不同的激活函数。
激活函数根据输入增强或抑制某些神经元。将其与人类大脑相比较,每当你要执行某些任务时,并非自出生以来存储的所有神经元或记忆都会被激发!只有相关的神经元被激发,而其余的则受到抑制。在数学领域,各种类型的激活函数执行此操作。但首先让我们看一下神经网络执行的两大类任务:
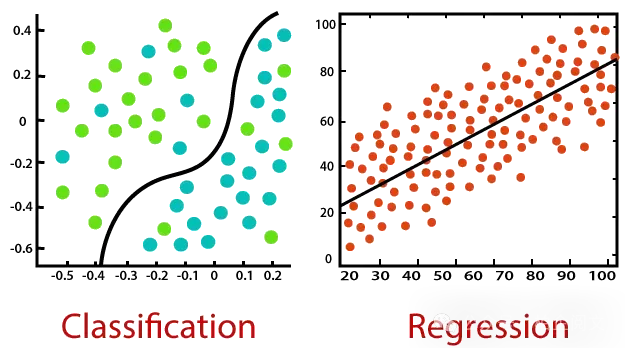
神经网络的两个主要目标:分类与回归
通常来说,分类和回归是两类最终需求。分类是指对一个问题给出是或否的答案,或者判断图片中的某个物体属于哪一类(比如狗、猫),而回归则意味着最终得到某个确定的值,例如,明天的股票点数会是多少,或者美元的价格会是多少。
 图片
图片
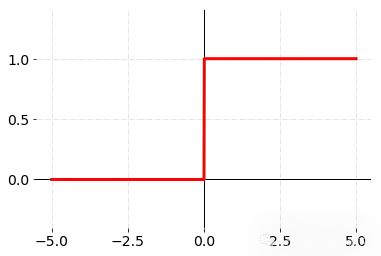
步长函数的问题:有限的开端
让我们回溯到神经网络的萌芽时期。最初使用的激活函数是阶跃函数——一种严格的开/关开关。它模仿生物神经元,当输入超过阈值时触发(输出为1),否则保持静默(输出为0)。
 图片
图片
虽然阶跃函数是一个有用的起点,但它有一些严重的局限性。
- 它在中心两侧的线性特性,严重限制了其在复杂、非线性现实生活问题中的应用。
- 它还有另一个致命缺陷:零学习信号。想象一下,教孩子数学时,只说“对”或“错”,却不解释错在哪里。阶跃函数的二元输出让优化器(与我们稍后将学习的神经网络训练相关)在训练过程中完全不知道如何调整权重。
- 它可能适用于分类任务,但在回归任务中会失败,因为所有值都会坍缩为0或1。
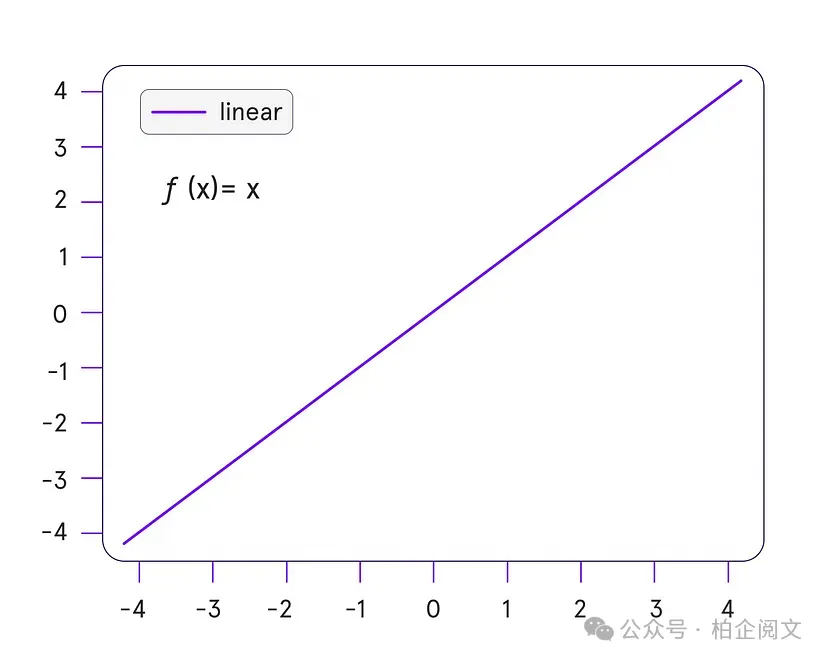
迈向辉煌的又一次尝试:线性激活
接下来是线性激活函数(y = x)。虽然它在回归任务(预测房价、温度)中表现出色,但在隐藏层却惨遭失败。为什么呢?堆叠的线性层会退化为一条直线(这是个由来已久的问题!)。无论你的网络有多深,它只能模拟直线关系——对于语音或图像等现实世界中的复杂情况毫无用处。它可能在某些非常特殊的情况下使用,但仅限于输出层。
 图片
图片
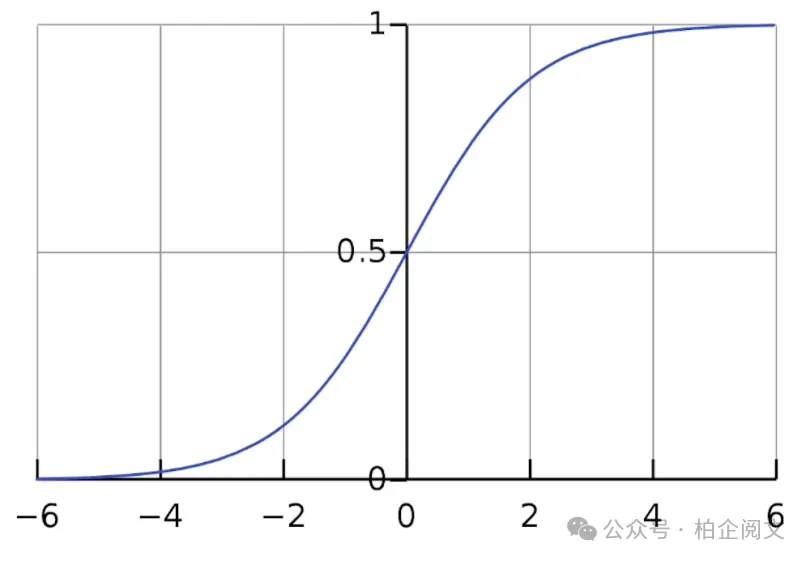
对更平滑过渡的追求:Sigmoid函数的兴起
对更好的激活函数的探索源于对更平滑过渡的渴望,关键是对可微性的渴望。阶跃函数的突然“跳跃”使得使用基于梯度下降的方法有效地训练神经网络变得困难(我们将在下一篇文章中探讨!)。为了解决这个问题,Sigmoid函数应运而生。这为获得0到1之间的连续输出铺平了道路,并且平滑的曲线有助于在X轴上的所有点进行求导。这使得神经网络能够应用梯度下降和反向传播技术。
 图片
图片
Sigmoid函数具有独特的S形曲线,是一种常用的替代选择。其公式如下:
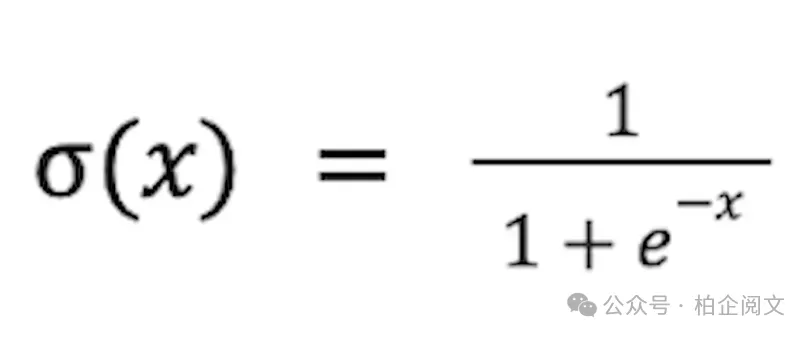 图片
图片
为什么Sigmoid函数如此具有吸引力?
- 平滑性与可微性:与阶跃函数不同,Sigmoid函数在任何地方都是平滑且可微的。这意味着我们可以计算输出相对于输入的梯度,这对于使用反向传播训练神经网络至关重要。
- 输出范围:Sigmoid函数将值压缩在0到1之间,为神经元的输出提供了概率解释。这使得它在二分类任务中特别有用,其中输出可以被解释为属于某个类别的概率。
- 模拟神经元放电(某种程度上):可以大致将Sigmoid函数解释为模拟生物神经元的放电速率。当输入较低时(神经元“不活跃”),它会产生一个接近0的值;当输入较高时(神经元“活跃”),它会产生一个接近1的值。
Sigmoid函数的兴衰:挑战浮现尽管Sigmoid函数最初取得了成功,但它最终也面临着一系列自身的挑战。随着神经网络变得越来越深且复杂,诸如梯度消失之类的问题开始浮现。
想象一下,一个信号在一长串神经元中传递。如果每个神经元都应用Sigmoid激活函数,信号的梯度(即输出相对于输入的变化量)往往会随着每一层的传递而缩小。这是因为Sigmoid函数的导数通常小于1。
随着梯度减小,网络中较早的层越来越难以有效地学习。这种现象被称为梯度消失问题,它限制了使用Sigmoid激活函数训练深度神经网络的能力。Sigmoid函数的另一个问题是输出不是以零为中心。所有神经元接收到的信号要么是正数,要么是零,这使得反向传播过程中的梯度更新要么为正,要么为负,从而导致训练过程呈之字形。
一股清新空气:ReLU变革
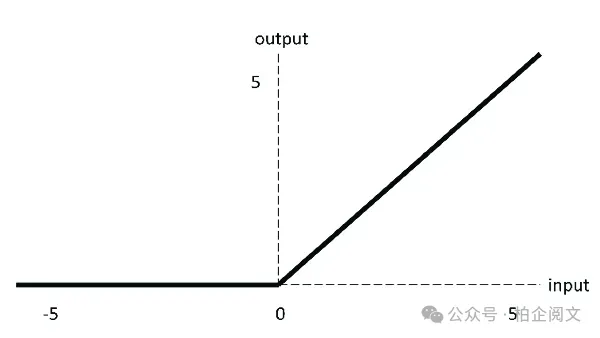
为了解决梯度消失问题并加速训练,以修正线性单元(ReLU)为首的新一代激活函数应运而生。ReLU函数看似简单:
换句话说,如果输入为正数,ReLU直接输出该输入。如果输入为负数,ReLU输出零。
 图片
图片
为什么ReLU变得如此流行?
- 应对梯度消失问题:ReLU函数对于正输入的导数为1,这有助于缓解梯度消失问题。这使得梯度能够更轻松地在网络中流动,从而实现更快、更有效的训练,尤其是在深度架构中。
- 简单性与高效性:ReLU函数在计算上非常高效。其简单的max(0, x)运算比Sigmoid和Tanh函数中涉及的指数运算要快得多。
- 稀疏性:ReLU倾向于产生稀疏激活,这意味着许多神经元输出为零。这种稀疏性有助于减少过拟合并提高泛化能力。零值有助于根据所需的计算开启和关闭神经元,从而实现有效的学习。
ReLU的怪癖:死亡ReLU与泄漏修正方案尽管ReLU有诸多优点,但它也并非毫无缺陷。一个潜在的问题是ReLU神经元死亡问题。如果一个ReLU神经元陷入其输入始终为负的状态,它将始终输出零,其梯度也将为零。这个神经元实际上就“死亡”了,不再学习。

 图片
图片
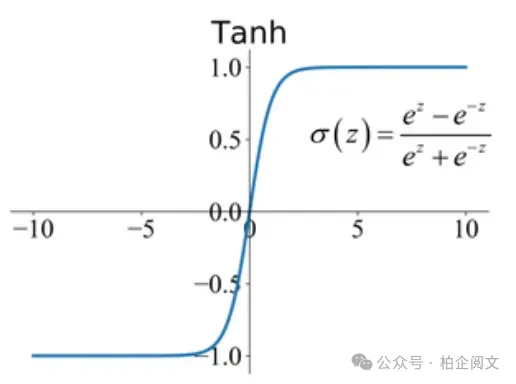
通过在神经元输入为负时允许少量梯度流过神经元,带泄漏修正线性单元(Leaky ReLU)和参数化修正线性单元(PReLU)有助于防止神经元死亡并提高学习稳定性。
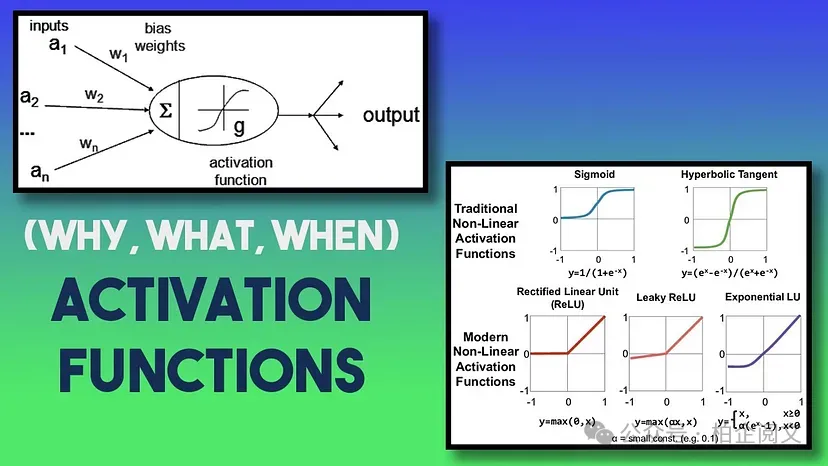
超越Sigmoid和ReLU:一个多样化的生态系统
激活函数的领域远不止于Sigmoid和ReLU。研究人员不断探索新的激活函数,每个函数都有其独特的属性和预期的应用场景。以下是一些值得注意的例子:
- 双曲正切函数(Tanh):Tanh是另一种S形激活函数,它将值压缩在-1到1之间。Tanh与Sigmoid函数类似,但它以零为中心,这有时可以使训练更快收敛。然而,它仍然存在梯度消失问题,尽管程度略小于Sigmoid函数。
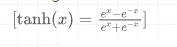
 图片
图片
- ELU(指数线性单元):ELU旨在结合ReLU和类Sigmoid函数的优点。对于正输入,它具有线性部分(类似于ReLU);对于负输入,它具有平滑的指数部分。ELU有助于缓解ReLU神经元死亡问题,有时能实现比ReLU更好的性能。
 图片
图片
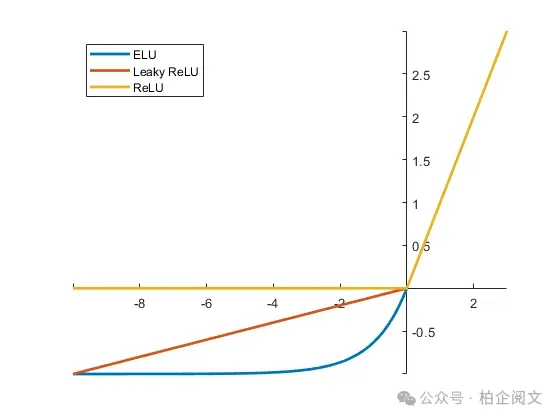
- Swish函数:Swish是一种相对较新的激活函数,由于其在各种深度学习任务中的出色表现而受到广泛关注。Swish函数的定义为:其中β是一个可学习参数或常数。Swish已被证明在深度网络中表现良好,有时性能优于ReLU和其他激活函数。
 图片
图片
- Softmax函数:虽然从技术上讲,Softmax函数并不在隐藏层中使用,但它在输出层处理多分类问题时至关重要。它将原始输出向量转换为不同类别上的概率分布,确保概率总和为1。
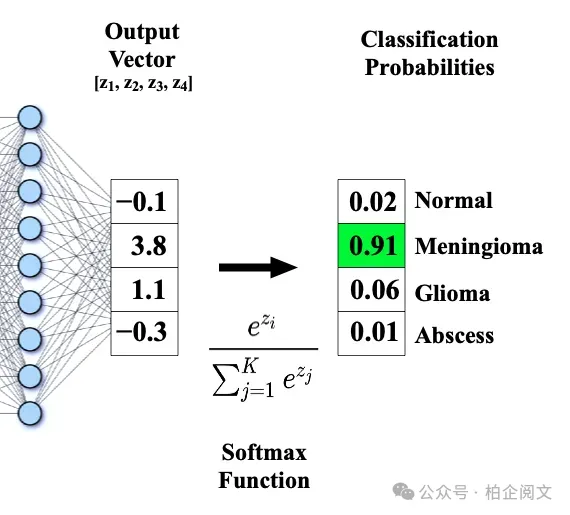 图片
图片
选择在你:挑选合适的激活函数
有这么多激活函数可供选择,你如何决定在神经网络中使用哪一个呢?没有放之四海而皆准的答案,最佳选择通常取决于具体的任务、网络架构和数据集。不过,这里有一些通用准则:
- 修正线性单元(ReLU)(及其变体):ReLU通常是许多任务的良好起点,尤其是在深度网络中。它计算效率高,有助于缓解梯度消失问题。如果你遇到ReLU死亡问题,可以考虑使用带泄漏修正线性单元(Leaky ReLU)或参数化修正线性单元(PReLU)。
- Sigmoid函数和双曲正切函数(Tanh):由于梯度消失问题,Sigmoid函数和双曲正切函数如今在隐藏层中使用较少。不过,在特定任务的输出层中,它们仍可能有用(例如,二元分类使用Sigmoid函数)。
- 实验是关键:确定最佳激活函数的最佳方法通常是通过实验。尝试不同的激活函数,并在验证集上比较它们的性能。
释放非线性潜力
激活函数远不止是数学上的奇思妙想;它们是神经网络智能化的关键推动者。通过引入非线性,它们使神经网络能够学习复杂的模式、模拟错综复杂的关系,并解决一系列仅靠线性模型无法解决的现实世界问题。从简单的阶跃函数到复杂的Swish函数,激活函数的演变一直是深度学习革命的驱动力。
Reference
[1] 加群链接: https://docs.qq.com/doc/DS3VGS0NFVHNRR0Ru#
[2] 知乎【柏企】: https://www.zhihu.com/people/cbq-91
[3] 个人网站: https://www.chenbaiqi.com