本文由东华大学蔡棽副教授、上海交通大学严骏驰教授和中国科学院自动化所申抒含研究员共同指导并撰写,四名学生作者为东华大学视觉与几何感知实验室的吴展豪、郭凌希、王佳纯、张斯禹。
一、论文简介
东华大学、上海交通大学、中科院自动化所的研究团队最新提出:两种基于几何的单应矩阵分解,极大地减少了四点求解单应的计算量(相比目前通用的求解稀疏线性方程组方法减少 95% 以上),可在二维码扫描等典型视觉应用中显著减少计算消耗,并有望应用于其他射影几何、计算机视觉和图形学问题中。
论文已被 IEEE T-PAMI 期刊接收。

- 论文标题:Fast and Interpretable 2D Homography Decomposition: Similarity-Kernel-Similarity and Affine-Core-Affine Transformations
- 论文主页链接(含论文、代码、视频介绍、奖金激励):http://www.cscvlab.com/research/SKS-Homography
二、问题介绍
平面单应,又称为二维射影变换,可表示为 3×3 的 8 自由度矩阵 (在相差一个尺度因子下)。源平面到目标平面的单应求解最小配置为 4 组对应点,每组对应点提供对
(在相差一个尺度因子下)。源平面到目标平面的单应求解最小配置为 4 组对应点,每组对应点提供对 的两个约束。记源平面
的两个约束。记源平面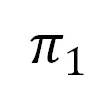 上的四个点为
上的四个点为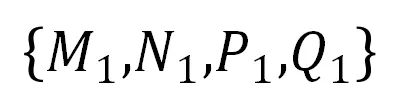 ,目标平面
,目标平面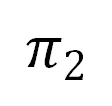 上的四个点为
上的四个点为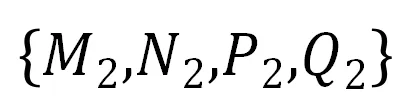 。一组对应点
。一组对应点 的齐次向量形式为
的齐次向量形式为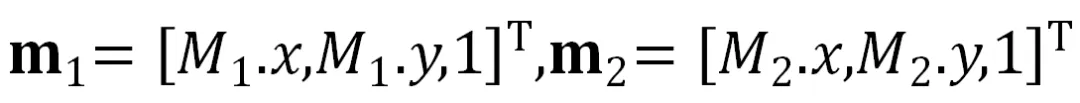 ,提供的约束可记为
,提供的约束可记为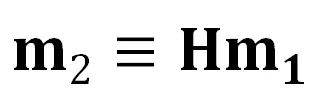 ,这里
,这里 表示齐次相等。
表示齐次相等。
以往的直接线性变换(Direct Linear Transformation, DLT)方法利用上述约束构建稀疏线性方程组进行单应求解,其中常用的一种非齐次线性方程组构建方法为:
令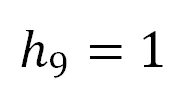 ,去除齐次性,可得
,去除齐次性,可得
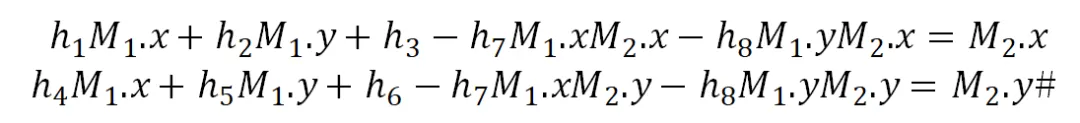
将 4 组点对的约束叠在一起,可得形如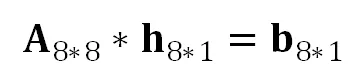 的稀疏线性方程组,并可通过对 8×8 系数矩阵的 LU 分解完成求解,在 OpenCV 库中实现此算法的计算量(浮点运算次数)约为 2000。
的稀疏线性方程组,并可通过对 8×8 系数矩阵的 LU 分解完成求解,在 OpenCV 库中实现此算法的计算量(浮点运算次数)约为 2000。
后续一些改进方法,利用了上面系数矩阵的稀疏特性,设计了:(1)简化的 3×3 系数矩阵的 SVD 分解,计算量约为 1800;(2)定制化的高斯消元法(放弃了选主元操作)求解,计算量约为 220。额外的,针对单应计算一类常见的应用场景 —— 扫描二维码,可简单地将源平面(二维码模版)的正方形四顶点坐标设置为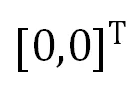 ,
,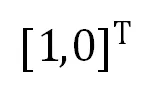 ,
,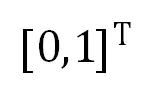 和
和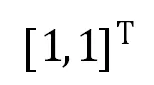 ,此时上述线性方程组的系数矩阵将进一步大幅化简,但未见过相关工作研究这种更为特殊线性方程组的简化求解。
,此时上述线性方程组的系数矩阵将进一步大幅化简,但未见过相关工作研究这种更为特殊线性方程组的简化求解。
三、本文方法
核心思想
基于几何变换的层次性(相似 - 仿射 - 射影),逐步利用部分点求出子变换,从而将单应矩阵分解为多个子变换完成分别求解并相乘。
- 【相似 - 相似射影核 - 相似(Similariry-Kernel-Similarity, SKS)变换】
如下图所示,SKS 利用两组对应点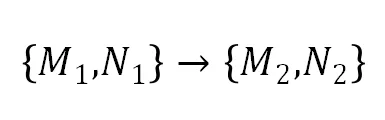 分别计算源、目标平面上的相似变换
分别计算源、目标平面上的相似变换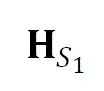 和
和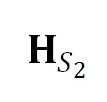 ,即将这两个点分别变换成标准点
,即将这两个点分别变换成标准点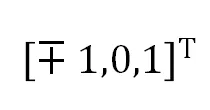 (齐次坐标表示)。
(齐次坐标表示)。 和
和 分别经过相似变换后,两个平面
分别经过相似变换后,两个平面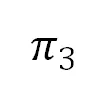 和
和 间的相似射影核变换
间的相似射影核变换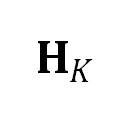 定义了射影畸变(形变)。进一步,
定义了射影畸变(形变)。进一步,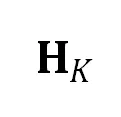 可被分解为若干变换的乘积,这里
可被分解为若干变换的乘积,这里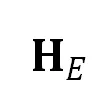 表示一个初等变换,将标准点变为直角双曲点;
表示一个初等变换,将标准点变为直角双曲点;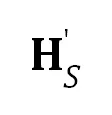 表示双曲相似变换,并可分解为两个平移,及表示双曲尺度和旋转的
表示双曲相似变换,并可分解为两个平移,及表示双曲尺度和旋转的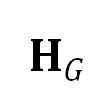 。
。
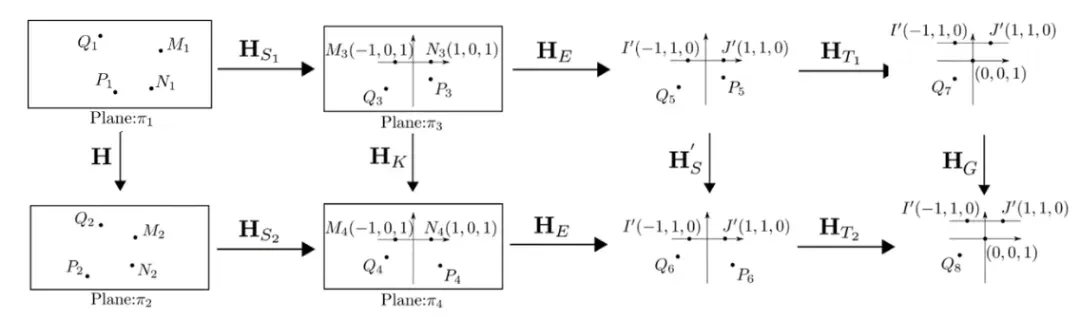
最终,单应矩阵 由上述 SKS 变换形成的分解形式为:
由上述 SKS 变换形成的分解形式为:
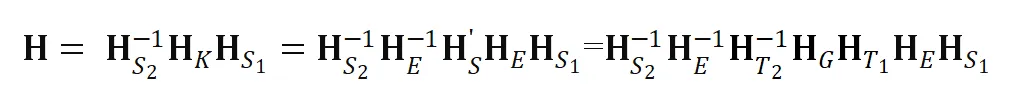
其中四参数的相似射影核变换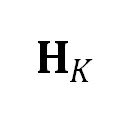 表示为
表示为
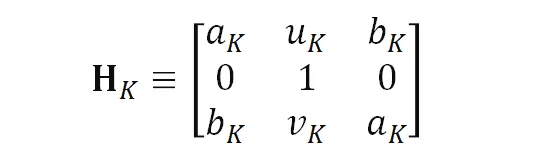
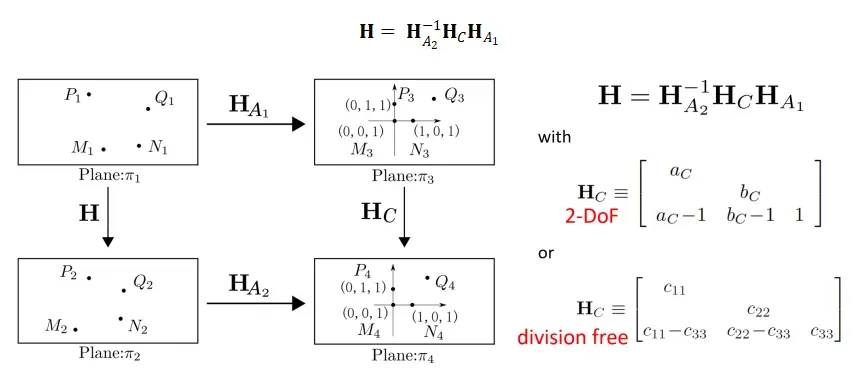
- 【仿射 - 仿射射影核 - 仿射(Affine-Core-Affine, ACA)变换】
类似地,可由三组对应点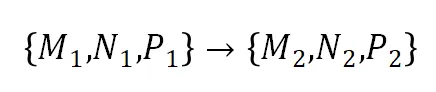 分别计算源、目标平面的仿射变换
分别计算源、目标平面的仿射变换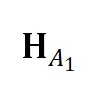 和
和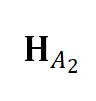 ,将它们分别变换为定义的标准点
,将它们分别变换为定义的标准点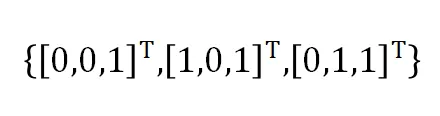 (齐次坐标表示)。如下图所示,平面
(齐次坐标表示)。如下图所示,平面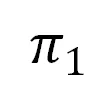 和
和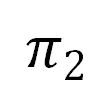 分别经过仿射变换后,平面
分别经过仿射变换后,平面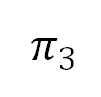 和
和 间的仿射射影核变换
间的仿射射影核变换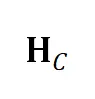 定义了射影畸变。如右侧所示,
定义了射影畸变。如右侧所示,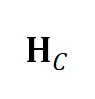 有两个自由度,因此可通过分别仿射变换后的第四组点对
有两个自由度,因此可通过分别仿射变换后的第四组点对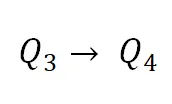 求得。在 ACA 变换下,单应矩阵分解为:
求得。在 ACA 变换下,单应矩阵分解为:
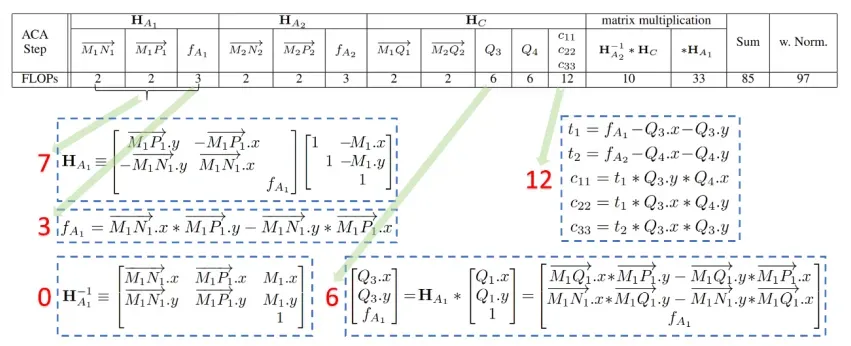
ACA 变换是极其高效的,其计算单应矩阵的浮点运算次数统计见下表。在相差一个比例因子下单应计算共计 85 次浮点运算。表下方同时给出了一些计算量统计的细节(可通过其中加、减、乘号的数目进行统计)。
- 【正方形模板的简化】
当四个源点构成一个特殊形状,ACA 算法的计算过程可以进一步简化。以下算法展示了矩形(或正方形)模版与其图像间单应的计算过程,分别需要 47 和 44 次浮点运算。
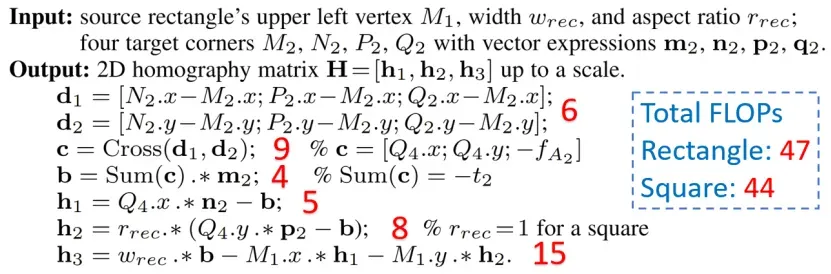
更进一步地,当使用正方形进行相机标定(聚焦于内参数)或二维码检测时,平面坐标系的位置通常无关紧要。一个简单的设置可假设左上角顶点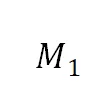 为原点,并且正方形的边长为 1(即宽高比
为原点,并且正方形的边长为 1(即宽高比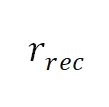 和宽度
和宽度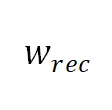 都为 1)。此时单应计算仅需 29 次浮点运算。
都为 1)。此时单应计算仅需 29 次浮点运算。
四、实验结果
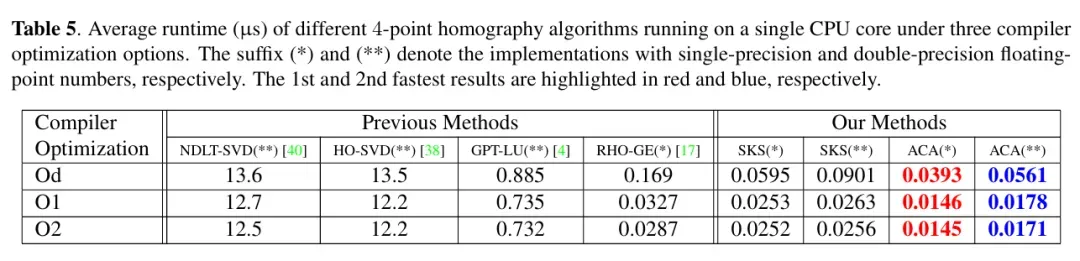
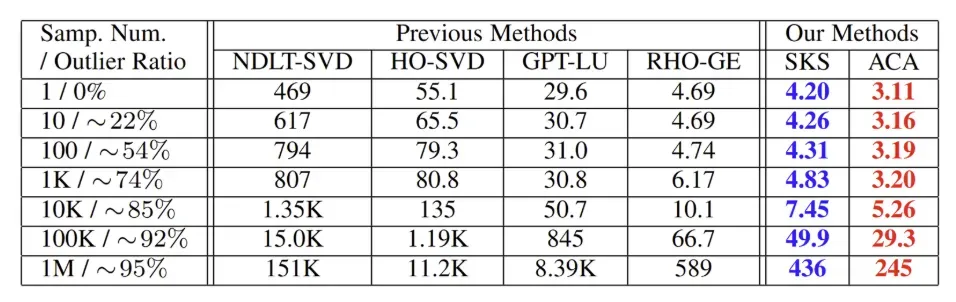
实验主要集中在评估 4 点单应求解器在不同场景下的运行时间,下面给出了 CPU 和 GPU 计算一个单应的平均运行时间对比。
更多的实验结果,如集成在 RANSAC 流程、集成在深度单应估计网络中求取单应,详见论文原文。
结果显示,使用双精度浮点数,ACA 分解完成一次四点单应计算的平均时间仅为 17 纳秒。与 DLT+LU 相比,SKS 和 ACA 在开启编译器默认的 O2 优化下分别实现了 29 倍和 43 倍的实际加速比。这两个数值远超理论上 FLOPs 的 11 倍和 20 倍比值,部分因为以往方法的实现涉及条件判断、数据拷贝等操作拖慢了执行速度,而这些操作并没有被 FLOPs 统计所覆盖。
五、总结与展望
平面单应计算可广泛应用于相机标定、图像拼接、增强现实、三维重建等视觉任务中,因此本方法可集成在众多视觉处理程序中,替换以往的单应算法。更为常见的是,二维码扫描中需要计算正方形(原始二维码模版)到其图像的单应,以校正图像后进行二维码信息解码。据估算目前中国的日均二维码扫描已达百亿次,本文提出计算正方形模版的单应仅需 29 次浮点运算,因此相比传统的 DLT+LU 方法,每天可减少浮点运算量约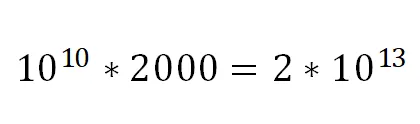 。
。
作为一项几何视觉理论研究,本文提出的 SKS 与 ACA 方法可广泛应用于基于平面的视觉或图形学任务中。目前,研究团队在深度学习估计单应的几何参数、基于平面单应的 P3P 姿态估计、N 维单应矩阵分解等问题开展了后续研究,取得了一些初步成果。



